
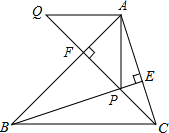
【题目】如图,BE、CF是△ABC的高且相交于点P,AQ∥BC交CF延长线于点Q,若有BP=AC,CQ=AB,线段AP与AQ的关系如何?说明理由。
【答案】证明见解析
【解析】试题分析:
由BE、CF是△ABC的高,易得∠ABP+∠BPF=90°,∠ACP+∠CPE=90°,结合∠BPF=∠CPE,易得∠ABP=∠ACP,这样结合BP=AC,CQ=AB,即可由“SAS”证得△ACQ≌△PBA,从而可得AP=AQ,∠Q=∠PAF,结合∠PAF+∠APF=90°,可得:∠APF+∠Q=90°,即可得到∠QAP=90°,从而可得AQ⊥AP,由此即可得到AQ与AP的关系是相等且互相垂直.
试题解析:
AQ与AP的关系是:相等且互相垂直,理由如下:
∵BE、CF是△ABC的高,
∴∠BFP=∠CEP=90°,
∴∠ABP+∠BPF=90°,∠ACP+∠CPE=90°,
又∵∠BPF=∠CPE,
∴∠ABP=∠ACP,
在△ACQ和△PBA中:
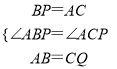 ,
,
∴△ACQ≌△PBA(SAS),
∴AP=AQ,∠Q=∠PAF,
∵∠PAF+∠APF=90°,
∴∠APF+∠Q=90°,
∴AP⊥AQ,即:AQ与AP的关系是相等且互相垂直.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,OE平分∠BOD,∠AOC=72°,∠DOF=90°.
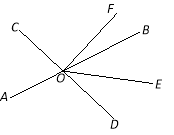
(1)写出图中任意一对互余的角;
(2)求∠EOF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】全世界人民踊跃为四川汶川灾区人民捐款,到6月3日止各地共捐款约424亿元,用科学记数法表示约为( )元.(保留两个有效数字)
A.4.23×1010
B.4.24×1010
C.4.24×1011
D.4.23×1011
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究题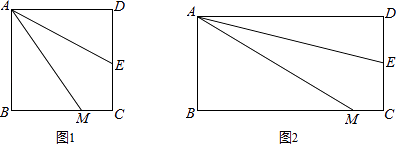
【问题情境】
如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.
(1)【探究展示】
直接写出AM、AD、MC三条线段的数量关系:;
(2)【拓展延伸】
AM=DE+BM是否成立?若成立,请给出证明;若不成立,请说明理由.
(3)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,探究展示(1)、(2)中的结论是否成立?请分别作出判断,不需要证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据科学研究表明,在弹簧的承受范围内,弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂的物体的重量x(kg)间有下表的关系:下列说法不正确的是( )
x/kg | 0 | 1 | 2 | 3 | 4 | 5 |
y/cm | 20 | 20.5 | 21 | 21.5 | 22 | 22.5 |
A. 弹簧不挂重物时的长度为0cm
B. x与y都是变量,且x是自变量,y是因变量
C. 随着所挂物体的重量增加,弹簧长度逐渐边长
D. 所挂物体的重量每增加1kg,弹簧长度增加0.5cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若数据x1,x2,…,xn的众数为a,方差为b,则数据x1+2,x2+2,…,xn+2的众数,方差分别是( )
A. a,bB. a,b+2C. a+2,bD. a+2,b+2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com