
【题目】某商店经营甲、乙两种商品,其进价和售价如下表:
甲 | 乙 | |
进价(元/件) | 15 | 35 |
售价(元/件) | 20 | 45 |
已知该商店购进了甲、乙两种商品共160件.
(1)若商店在销售完这批商品后要获利1000元,则应分别购进甲、乙两种商品各多少件?
(2)若商店的投入资金少于4300元,且要在售完这批商品后获利不少于1250元,则共有几种购货的方案?其中,哪种购货方案获得的利润最大?
【答案】(1)甲、乙两种商品分别购进了120件、40件;(2)5种购货的方案,甲购进66件、乙购进94件获得的利润最大.
【解析】
试题(1)等量关系为:甲件数+乙件数=160;甲总利润+乙总利润=1100.
(2)设出所需未知数,甲进价×甲数量+乙进价×乙数量≤4300.
试题解析:(1)设商店甲、乙两种商品分别购进了x件、y件,
由题意得
![]()
解得![]()
答:商店甲、乙两种商品分别购进了120件、40件;
(2)设商店甲商品购进了z件,则乙商品购进了(160-z)件,
由题意得:
![]()
解得 65<z≤70
∴z的整数值为66,67,68,69,70.
即共有5种购货的方案:
①甲购进66件、乙购进94件,
②甲购进67件、乙购进93件,
③甲购进68件、乙购进98件,
④甲购进69件、乙购进91件,
⑤甲购进70件、乙购进90件.
其中,购货方案①获得的利润最大.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】网瘾低龄化问题已经引起社会各界的高度关注,有关部门在全国范围内对12﹣35岁的网瘾人群进行了简单的随机抽样调查,绘制出以下两幅统计图.

请根据图中的信息,回答下列问题:
(1)这次抽样调查中共调查了 人;
(2)请补全条形统计图;
(3)扇形统计图中18﹣23岁部分的圆心角的度数是 ;
(4)据报道,目前我国12﹣35岁网瘾人数约为2000万,请估计其中12﹣23岁的人数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长度为_____
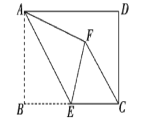
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校组织![]() 名同学和
名同学和![]() 名教师参加校外学习交流活动现打算选租大、小两种客车,大客车载客量为
名教师参加校外学习交流活动现打算选租大、小两种客车,大客车载客量为![]() 人/辆,小客车载客量为
人/辆,小客车载客量为![]() 人/辆
人/辆
(1)学校准备租用![]() 辆客车,有几种租车方案?
辆客车,有几种租车方案?
(2)在(1)的条件下,若大客车租金为![]() 元/辆,小客车租金为
元/辆,小客车租金为![]() 元/辆,哪种租车方案最省钱?
元/辆,哪种租车方案最省钱?
(3)学校临时增加![]() 名学生和
名学生和![]() 名教师参加活动,每辆大客车有2名教师带队,每辆小客车至少有
名教师参加活动,每辆大客车有2名教师带队,每辆小客车至少有![]() 名教师带队.同学先坐满大客车,再依次坐满小客车,最后一辆小客车至少要有
名教师带队.同学先坐满大客车,再依次坐满小客车,最后一辆小客车至少要有![]() 人,请你帮助设计租车方案
人,请你帮助设计租车方案
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,若AB=1,BC=2,则△ABE和△BC′F的周长之和为( )

A. 3 B. 4 C. 6 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某农场有A、B两种型号的收割机共20台,每台A型收割机每天可收大麦100亩或者小麦80亩,每台B型收割机每天可收大麦80亩或者小麦60亩,该农场现有19 000亩大麦和11 500亩小麦先后等待收割.先安排这20台收割机全部收割大麦,并且恰好10天时间全部收完.
(1)问A、B两种型号的收割机各多少台?
(2)由于气候影响,要求通过加班方式使每台收割机每天多完成10%的收割量,问这20台收割机能否在一周时间内完成全部小麦收割任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF.
(1)求证:AD平分∠BAC.
(2)写出AB+AC与AE之间的等量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象经过点(-2,0),(x0,0),1<x0<2,与y轴的负半轴相交,且交点在(0,-2)的上方,下列结论:
①b>0;②2a<b;③2a-b-1<0;④2a+c<0.其中正确结论是 _________(填正确序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com