
【题目】二次函数y=ax2+bx+c(a≠0)的图象经过点(-2,0),(x0,0),1<x0<2,与y轴的负半轴相交,且交点在(0,-2)的上方,下列结论:
①b>0;②2a<b;③2a-b-1<0;④2a+c<0.其中正确结论是 _________(填正确序号)
科目:初中数学 来源: 题型:
【题目】某商店经营甲、乙两种商品,其进价和售价如下表:
甲 | 乙 | |
进价(元/件) | 15 | 35 |
售价(元/件) | 20 | 45 |
已知该商店购进了甲、乙两种商品共160件.
(1)若商店在销售完这批商品后要获利1000元,则应分别购进甲、乙两种商品各多少件?
(2)若商店的投入资金少于4300元,且要在售完这批商品后获利不少于1250元,则共有几种购货的方案?其中,哪种购货方案获得的利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)阅读理解:课外兴趣小组活动时,老师提出了如下问题:
在△ABC中,AB=9,AC=5,求BC边上的中线AD的取值范围。
小明在组内经过合作交流,得到了如下的解决方法(如图1):
①延长AD到Q,使得DQ=AD;
②再连接BQ,把AB、AC、2AD集中在△ABQ中;
③利用三角形的三边关系可得4<AQ<14,则AD的取值范围是_____________。
感悟:解题时,条件中若出现“中点”“中线”等条件,可以考虑倍长中线,构造全等三角形,把分散的己知条件和所求证的结论集中到同一个三角形中。
(2)请你写出图1中AC与BQ的位置关系并证明。
(3)思考:已知,如图2,AD是△ABC的中线,AB=AE,AC=AF,∠BAE=∠FAC=90°。试探究线段AD与EF的数量和位置关系并加以证明。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解社区居民最喜欢的支付方式,某兴趣小组对龙湖社区内20~60岁年龄段的部分居民展开了随机问卷调查(每人只能选择其中一项),并将调查数据整理后绘成如下两幅不完整的统计图.请根据图中信息解答下列问题:

(1)求参与问卷调查的总人数.
(2)补全条形统计图.
(3)该社区中20~60岁的居民约4000人,估算这些人中最喜欢微信支付方式的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
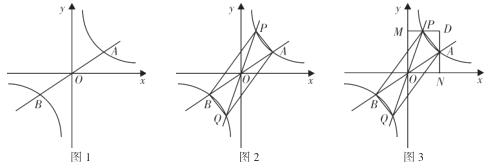
如图1,正比例函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() 、
、![]() .我们可以发现:反比例函数
.我们可以发现:反比例函数![]() 的图象是一个关于原点中心对称的图形.
的图象是一个关于原点中心对称的图形.
(1)填空:![]() ,
,![]() ,
,![]() ,
,![]() ;
;
(2)利用所给函数图象,写出不等式![]() 的解集 ;
的解集 ;
(3)如图2,正比例函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() 、
、![]() .试说明以
.试说明以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形一定是平行四边形,但不可能是正方形;
为顶点的四边形一定是平行四边形,但不可能是正方形;
(4)如图3,当点![]() 在点
在点![]() 的左上方时,过
的左上方时,过![]() 作直线
作直线![]() 轴于点
轴于点![]() ,过点
,过点![]() 作直线
作直线轴于点
![]() ,交直线
,交直线![]() 于点
于点![]() ,若四边形
,若四边形![]() 的面积为
的面积为![]() .求点
.求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,AC、DC为弦,∠ACD=60°,P为AB延长线上的点,∠APD=30°.

(1)求证:DP是⊙O的切线;
(2)若⊙O的半径为3cm,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AD是△ABC的中线,AE⊥AB,AF⊥AC,且AE=AB,AF=AC,AD=3,AB=4.

(1)求AC长度的取值范围;
(2)求EF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请你画出一个以BC为底边的等腰ΔABC,使底边上的高AD=BC.
(1)求tanB和 sinB的值;
(2)在你所画的等腰ΔABC中设底边BC=5米,求腰上的高BE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com