
【题目】综合与实践
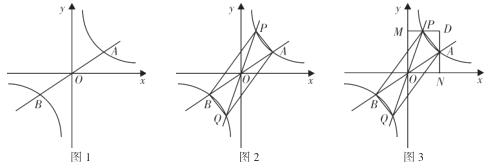
如图1,正比例函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() 、
、![]() .我们可以发现:反比例函数
.我们可以发现:反比例函数![]() 的图象是一个关于原点中心对称的图形.
的图象是一个关于原点中心对称的图形.
(1)填空:![]() ,
,![]() ,
,![]() ,
,![]() ;
;
(2)利用所给函数图象,写出不等式![]() 的解集 ;
的解集 ;
(3)如图2,正比例函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() 、
、![]() .试说明以
.试说明以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形一定是平行四边形,但不可能是正方形;
为顶点的四边形一定是平行四边形,但不可能是正方形;
(4)如图3,当点![]() 在点
在点![]() 的左上方时,过
的左上方时,过![]() 作直线
作直线![]() 轴于点
轴于点![]() ,过点
,过点![]() 作直线
作直线轴于点
![]() ,交直线
,交直线![]() 于点
于点![]() ,若四边形
,若四边形![]() 的面积为
的面积为![]() .求点
.求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;
;![]() ;
;![]() ;
;![]() ;(2)
;(2)![]() 或
或![]() ;(3)见解析;(4)点
;(3)见解析;(4)点![]() 的坐标为
的坐标为![]()
【解析】
(1)由题意直接把点A(3,2)代入一次函数及反比例函数的解析式求出k1及a的值,再根据反比例函数的图象关于原点对称可得出m、n的值;
(2)由题意直接根据两函数的图象即可得出结论;
(3)根据题意利用“反比例函数的图象是一个关于原点中心对称的图形”得:OA=OB,OP=OQ,故以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形的对角线互相平分,所以以
为顶点的四边形的对角线互相平分,所以以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形一定是平行四边形,并由
为顶点的四边形一定是平行四边形,并由![]() ,对角线
,对角线![]() 与
与![]() 不可能互相垂直,即可得出以
不可能互相垂直,即可得出以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形不可能是菱形,也就不可能是正方形;
为顶点的四边形不可能是菱形,也就不可能是正方形;
(4)根据题意设点![]() ,由题意可知四边形
,由题意可知四边形![]() 是矩形,故可得出OM×PM=6,ON×AN=6,根据
是矩形,故可得出OM×PM=6,ON×AN=6,根据![]() 可得出其面积,
可得出其面积,![]() 可求出ONOM的值,由此可得出结论.
可求出ONOM的值,由此可得出结论.
解:(1)∵正比例函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点A(3,2),
的图象交于点A(3,2),
∴![]() ,解得
,解得![]() ,解得a=6.
,解得a=6.
∵正比例函数与反比例函数的图象均关于原点对称,
∴B(-3,-2),
∴m=-3,n=-2.
故答案为:![]() ;
;![]() ;
;![]() ;
;![]() .
.
(2)∵A(3,2)、B(-3,-2),
∴当x<-3或0<x<3时,![]() .
.
故答案为:x<-3或0<x<3.
(3)∵反比例函数的图象是一个关于原点中心对称的图形,
∴![]() ,
,![]() ,
,
∴以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形的对角线互相平分,所以以
为顶点的四边形的对角线互相平分,所以以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形一定是平行四边形.
为顶点的四边形一定是平行四边形.
∵点![]() 、
、![]() 都在第一象限,
都在第一象限,
∴![]() ,对角线
,对角线![]() 与
与![]() 不可能互相垂直,
不可能互相垂直,
∴以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形不可能是菱形,也就不可能是正方形.
为顶点的四边形不可能是菱形,也就不可能是正方形.
(4)设点![]() ,由题意可知四边形
,由题意可知四边形![]() 是矩形.
是矩形.
∵![]() 和
和![]() 都在双曲线上,
都在双曲线上,
∴![]() ,
,![]() ,
,
∴![]() ,
,
又![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,![]() ,
,
∴点![]() 的坐标为
的坐标为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,若AB=1,BC=2,则△ABE和△BC′F的周长之和为( )

A. 3 B. 4 C. 6 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在正方形![]() 中,点
中,点![]() 分别在
分别在![]() 上,△
上,△![]() 是等边三角形,连接
是等边三角形,连接![]() 交
交![]() 于
于![]() ,给出下列结论:
,给出下列结论:
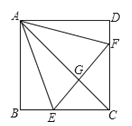
①![]() ; ②
; ② ![]() ;
;
③![]() 垂直平分
垂直平分![]() ; ④
; ④![]() .
.
其中结论正确的共有( ).
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象经过点(-2,0),(x0,0),1<x0<2,与y轴的负半轴相交,且交点在(0,-2)的上方,下列结论:
①b>0;②2a<b;③2a-b-1<0;④2a+c<0.其中正确结论是 _________(填正确序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】山西民间的雕刻艺术源远流长,主要以古代传统吉祥纹样为素材,以石雕、木雕砖雕等形式,来体现主人的高尚情操和文化修养以及人们的美好愿望.某木雕经销商购进“木象”和“木马”两种雕刻艺术品,购“木象”艺术品共用了![]() 元,“木马”艺术品共用了
元,“木马”艺术品共用了![]() 元已知“木马”每件的进价比“木象”每件的进价贵
元已知“木马”每件的进价比“木象”每件的进价贵![]() 元,且购进“木象”“木马”的数量相同.
元,且购进“木象”“木马”的数量相同.

![]() 求每件“木象”、“木马”艺术品的进价;
求每件“木象”、“木马”艺术品的进价;
![]() 该经销商将购进的两种艺术品进行销售,“木象”的销售单价为
该经销商将购进的两种艺术品进行销售,“木象”的销售单价为![]() 元,“木马”的销售单价为
元,“木马”的销售单价为![]() 元,销售过程中发现“木象”的销量不好,经销商决定:“木象”销售一定数量后,将剩余的“木象”按原销售单价的七折销售;“木马”的销售单价保持不变要使两种艺术品全部售完后共获利不少于
元,销售过程中发现“木象”的销量不好,经销商决定:“木象”销售一定数量后,将剩余的“木象”按原销售单价的七折销售;“木马”的销售单价保持不变要使两种艺术品全部售完后共获利不少于![]() 元,问“木象”按原销售单价应至少销售多少件?
元,问“木象”按原销售单价应至少销售多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
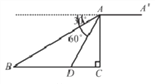
【题目】如图,某无人机于空中A处探测到目标B、D的俯角分别是30°、60°,此时无人机的飞行高度AC为60m.随后无人机从A处继续水平飞行30![]() m到达A′处.
m到达A′处.
(1)求A、B之间的距离:
(2)求从无人机A′上看目标D的俯角的正切值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com