
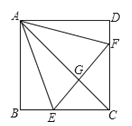
【题目】如图,已知在正方形![]() 中,点
中,点![]() 分别在
分别在![]() 上,△
上,△![]() 是等边三角形,连接
是等边三角形,连接![]() 交
交![]() 于
于![]() ,给出下列结论:
,给出下列结论:
①![]() ; ②
; ② ![]() ;
;
③![]() 垂直平分
垂直平分![]() ; ④
; ④![]() .
.
其中结论正确的共有( ).
A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】试题解析:∵四边形ABCD是正方形,
∴AB=AD,
∵△AEF是等边三角形,
∴AE=AF,
在Rt△ABE和Rt△ADF中,![]() ,
,
∴Rt△ABE≌Rt△ADF(HL),
∴BE=DF,
∴①说法正确;
∵BC=DC,
∴BC-BE=CD-DF,
∴CE=CF,
∴△ECF是等腰直角三角形,
∴∠CFE=45°,
∴∠AFD=75°,
∴∠DAF=15°,
∴②正确;
∵AC是正方形ABCD的对角线,∴∠BCA=45°,
∴AC⊥EF,
又CE=CF,
∴AC垂直平分EF,
∴③正确;
在AD上取一点G,连接FG,使AG=GF,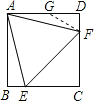
则∠DAF=∠GFA=15°,
∴∠DGF=2∠DAF=30°,
设DF=1,则AG=GF=2,DG=![]() ,
,
∴AD=CD=![]() ,CF=CE=CD-DF=
,CF=CE=CD-DF=![]() ,
,
∴![]() ,而BE+DF=2,
,而BE+DF=2,
∴④说法错误;
综上所述,正确的个数有3个.故本题应选C.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2+bx+c经过A(1,0),B(0,2)两点,顶点为D.
(1)求抛物线的解析式;
(2)将△OAB绕点A顺时针旋转90°后,点B落到点C的位置,将抛物线沿y轴平移后经过点C,求平移后所得图象的函数关系式;
(3)设(2)中平移后,所得抛物线与y轴的交点为B1,顶点为D1,若点N在平移后的抛物线上,且满足△NBB1的面积是△NDD1面积的2倍,求点N的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学课上,老师给出这样一个问题:
如图1,在平行四边形ABCD中,AB<BC.利用尺规作图,在边BC上确定一点E为圆心作圆,使⊙E与边AB,AD都相切(不写作法,保留作图痕迹);
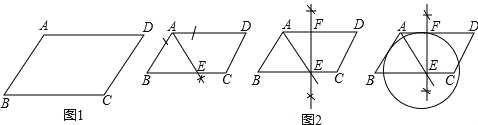
小刚是这样思考的:(如图2)
(1)作∠BAD的平分线与BC边交于点E;
(2)过点E作边AD的垂线,垂足为点F;
(3)以点E为圆心,EF长为半径作圆即可;
小刚把想法和老师交流了,得到了老师的肯定和赞扬,请你回答:小刚这样做的依据是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列语句正确的是( )
A.相等的角是对顶角
B.不是对顶角的角都不相等.
C.不相等的角一定不是对顶角
D.有公共点且和为180°的两个角是对顶角.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com