【题目】已知等腰三角形的腰长为10，一腰上的高为6，则以底边为边长的正方形的面积为_______．
【答案】360或40
【解析】本题注意画出△ABC图形分情况讨论,当△ABC为锐角等腰三角形时, AB=AC为腰,过点C作腰AB的高CD将△ABC分成两个直角三角形分别是:Rt△ADC和Rt△BDC,在Rt△ADC中,已知AC=10,CD=6,根据勾股定理得AD=
,则BD=10-8=2,在Rt△BDC中, 已知BD=2,CD=6,根据勾股定理得BC=
,此时以底边BC为边长的正方形的面积为40； 当△ABC为锐角等腰三角形时, AB=AC为腰,过点C作腰BA延长线上的高CD，CD与AC和BC分别构成:Rt△ADC和Rt△BDC, Rt△ADC中,已知AC=10,CD=6,根据勾股定理得AD=, BD=10+8=18, 在Rt△BDC中, 已知BD=18,CD=6,根据勾股定理得BC=
,此时以底边BC为边长的正方形的面积为360.
阅读快车系列答案科目：初中数学 来源： 题型：
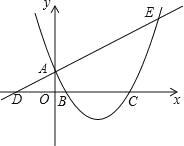
【题目】如图，已知直线y=
x+1与y轴交于点A，与x轴交于点D，抛物线y=x2+bx+c与直线交于A、E两点，与x轴交于B、C两点，且B点坐标为（1，0）．
（1）求该抛物线的解析式；
（2）在抛物线的对称轴上找一点M，使|AM﹣MC|的值最大，求出点M的坐标；
（3）动点P在x轴上移动，当△PAE是直角三角形时，求点P的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知在正方形
中，点
分别在
上，△
是等边三角形，连接
交
于
，给出下列结论：
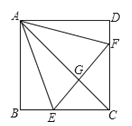
①
； ② 
;
③
垂直平分
; ④
．
其中结论正确的共有( )．
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】潜水艇上浮记为正，下潜记为负，若潜水艇原来在距水面50米深处，后来两次活动记录的情况分别是﹣20米，+10米，那么现在潜水艇在距水面_____米深处．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图,有一块塑料矩形模板ABCD，长为10cm，宽为4cm，将你手中足够大的直角三角板 PHF 的直角顶点P落在AD边上(不与A、D重合)，在AD上适当移动三角板顶点P:
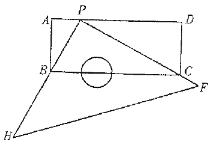
①能否使你的三角板两直角边分别通过点B与点C?若能，请你求出这时 AP 的长；若不能，请说明理由；
②再次移动三角板位置，使三角板顶点P在AD上移动，直角边PH 始终通过点B，另一直角边PF与DC的延长线交于点Q，与BC交于点E，能否使CE=2cm?若能，请你求出这时AP的长；若不能，请你说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com