
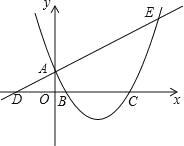
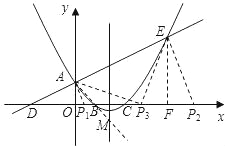
【题目】如图,已知直线y=![]() x+1与y轴交于点A,与x轴交于点D,抛物线y=x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为(1,0).
x+1与y轴交于点A,与x轴交于点D,抛物线y=x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为(1,0).
(1)求该抛物线的解析式;
(2)在抛物线的对称轴上找一点M,使|AM﹣MC|的值最大,求出点M的坐标;
(3)动点P在x轴上移动,当△PAE是直角三角形时,求点P的坐标.
【答案】(1)、y=x2﹣x+1;(2)、M(![]() ,﹣
,﹣![]() );(3)、(
);(3)、(![]() ,0)或(1,0)或(3,0)或(
,0)或(1,0)或(3,0)或(![]() ,0)
,0)
【解析】
试题分析:(1)、根据直线的解析式求得点A(0,1),那么把A,B坐标代入y=![]() x2+bx+c即可求得函数解析式.(2)、易得|AM﹣MC|的值最大,应找到C关于对称轴的对称点B,连接AB交对称轴的一点就是M.应让过AB的直线解析式和对称轴的解析式联立即可求得点M坐标.(3)、让直线解析式与抛物线的解析式结合即可求得点E的坐标.△PAE是直角三角形,应分点P为直角顶点,点A是直角顶点,点E是直角顶点三种情况探讨.
x2+bx+c即可求得函数解析式.(2)、易得|AM﹣MC|的值最大,应找到C关于对称轴的对称点B,连接AB交对称轴的一点就是M.应让过AB的直线解析式和对称轴的解析式联立即可求得点M坐标.(3)、让直线解析式与抛物线的解析式结合即可求得点E的坐标.△PAE是直角三角形,应分点P为直角顶点,点A是直角顶点,点E是直角顶点三种情况探讨.
试题解析:(1)、将A(0,1)、B(1,0)坐标代入y=x2+bx+c 得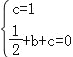 , 解得:
, 解得: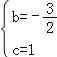 .
.
∴物线的解折式为y=x2﹣x+1;
(2)、抛物线的对称轴为x=![]() ,B、C关于x=
,B、C关于x=![]() 对称, ∴MC=MB,
对称, ∴MC=MB,
要使|AM﹣MC|最大,即是使|AM﹣MB|最大,
由三角形两边之差小于第三边得,当A、B、M在同一直线上时|AM﹣MB|的值最大.
知直线AB的解析式为y=﹣x+1 ∴ , 解得:
, 解得: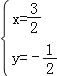 . 则M(
. 则M(![]() ,﹣
,﹣![]() ).
).
(3)、设点E的横坐标为m,则它的纵坐标为m2﹣m+1, 即E点的坐标(m,m2﹣m+1),
又∵点E在直线y=x+1上, ∴m2﹣m+1=m+1 解得m1=0(舍去),m2=4, ∴E的坐标为(4,3).
(Ⅰ)当A为直角顶点时, 过A作AP1⊥DE交x轴于P1点,设P1(a,0)易知D点坐标为(﹣2,0),
由Rt△AOD∽Rt△P1OA得 ![]() 即
即![]() , ∴a=
, ∴a=![]() ,a=-
,a=-![]() (舍去), ∴P1(
(舍去), ∴P1(![]() ,0).
,0).
(Ⅱ)同理,当E为直角顶点时,过E作EP2⊥DE交x轴于P2点,
由Rt△AOD∽Rt△P2ED得, ![]() 即:
即:![]() , ∴EP2=
, ∴EP2=![]() ∴DP2=
∴DP2=![]() =
=![]()
∴a=![]() ﹣2=
﹣2=![]() , ∴P2点坐标为(
, ∴P2点坐标为(![]() ,0).
,0).
(Ⅲ)当P为直角顶点时,过E作EF⊥x轴于F,设P3(b、0),
由∠OPA+∠FPE=90°,得∠OPA=∠FEP,Rt△AOP∽Rt△PFE,
由![]() 得:
得:![]() , 解得b1=3,b2=1, ∴此时的点P3的坐标为(1,0)或(3,0),
, 解得b1=3,b2=1, ∴此时的点P3的坐标为(1,0)或(3,0),
综上所述,满足条件的点P的坐标为(![]() ,0)或(1,0)或(3,0)或(
,0)或(1,0)或(3,0)或(![]() ,0).
,0).


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=7,AC=5,BC=6,∠ABC和∠ACB的平分线相交于点D,过点D作BC的平行线交AB于点E,交AC于点F.则△AEF的周长为( )

A.9 B.11 C.12 D.13
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是一个数值转换器,原理如图所示. 
(1)当输入的x值为16时,求输出的y值;
(2)是否存在输入的x值后,始终输不出y值?如果存在,请直接写出所有满足要求的x值;如果不存在,请说明理由.
(3)输入一个两位数x,恰好经过两次取算术平方根才能输出无理数,则x= .
查看答案和解析>>
科目:初中数学 来源: 题型:
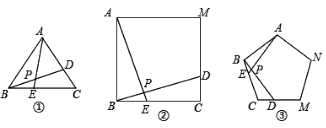
【题目】如图①、②、③中,点E、D分别是正△ABC、正四边形ABCM、正五边形ABCMN中以C点为顶点的相邻两边上的点,且BE=CD,DB交AE于P点.
(1)求图①中,∠APD的度数为_______;(2)图②中,∠APD的度数为_________,
(3)图③中,∠APD的度数为_______;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,最适合采用抽样调查的是( )
A. 对旅客上飞机前的安检 B. 了解全班同学每周体育锻炼的时间
C. 企业招聘,对应聘人员的面试 D. 了解某批次灯泡的使用寿命情况
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2+bx+c经过A(1,0),B(0,2)两点,顶点为D.
(1)求抛物线的解析式;
(2)将△OAB绕点A顺时针旋转90°后,点B落到点C的位置,将抛物线沿y轴平移后经过点C,求平移后所得图象的函数关系式;
(3)设(2)中平移后,所得抛物线与y轴的交点为B1,顶点为D1,若点N在平移后的抛物线上,且满足△NBB1的面积是△NDD1面积的2倍,求点N的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学课上,老师给出这样一个问题:
如图1,在平行四边形ABCD中,AB<BC.利用尺规作图,在边BC上确定一点E为圆心作圆,使⊙E与边AB,AD都相切(不写作法,保留作图痕迹);
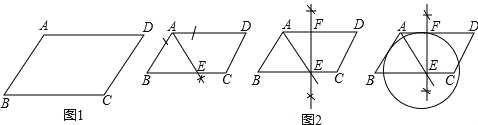
小刚是这样思考的:(如图2)
(1)作∠BAD的平分线与BC边交于点E;
(2)过点E作边AD的垂线,垂足为点F;
(3)以点E为圆心,EF长为半径作圆即可;
小刚把想法和老师交流了,得到了老师的肯定和赞扬,请你回答:小刚这样做的依据是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com