
【题目】如图①、②、③中,点E、D分别是正△ABC、正四边形ABCM、正五边形ABCMN中以C点为顶点的相邻两边上的点,且BE=CD,DB交AE于P点.
(1)求图①中,∠APD的度数为_______;(2)图②中,∠APD的度数为_________,
(3)图③中,∠APD的度数为_______;
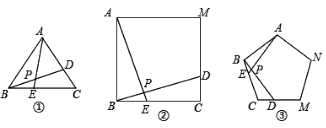
【答案】 60° 90° 108°
【解析】试题分析:(1)由观察图形可以看出∠APD是△APB的一个外角,∠APD=∠BAE+∠ABD.又可得出△ABE≌△BCD,由此便可求出∠APD=∠ABP+∠BAE=∠ABP+∠CBD=∠ABE=60°.
(2)同理,∠APD=∠M,即等于多边形的内角.
(3)同理,∠APD=∠BPE,即等于多边形的内角.
试题解析:(1)∵△ABC是等边三角形,
∴AB=BC,∠ABE=∠BCD=60°.
∵BE=CD,
∴△ABE≌△BCD.
∴∠BAE=∠CBD.
∴∠APD=∠ABP+∠BAE=∠ABP+∠CBD=∠ABE=60°.
(2)同理可证:△ABE≌△BCD,
∴∠AEB+∠DBC=180°-90°=90°,
∴∠APD=∠BPE=180°-90°=90°;
(3)同理可证△ABE≌△BCD,
∴∠AEB+∠DBC=180°-108°=72°,
∴∠APD=∠BPE=180°-72°=108°.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点F是BC延长线上一点,以CF为边,作菱形CDEF,使菱形CDEF与点A在BC的同侧,连接BE,点G是BE的中点,连接AG、DG.
(1)如图①,当∠BAC=∠DCF=90°时,直接写出AG与DG的位置和数量关系;
(2)如图②,当∠BAC=∠DCF=60°时,试探究AG与DG的位置和数量关系,
(3)当∠BAC=∠DCF=α时,直接写出AG与DG的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A,B在半径为1的⊙O上,∠AOB=60°,延长OB至C,过点C作直线OA的垂线记为l,则下列说法正确的是( )

A.当BC等于0.5时,l与⊙O相离
B.当BC等于2时,l与⊙O相切
C.当BC等于1时,l与⊙O相交
D.当BC不为1时,l与⊙O不相切
查看答案和解析>>
科目:初中数学 来源: 题型:
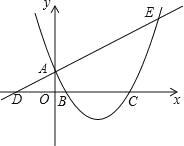
【题目】如图,已知直线y=![]() x+1与y轴交于点A,与x轴交于点D,抛物线y=x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为(1,0).
x+1与y轴交于点A,与x轴交于点D,抛物线y=x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为(1,0).
(1)求该抛物线的解析式;
(2)在抛物线的对称轴上找一点M,使|AM﹣MC|的值最大,求出点M的坐标;
(3)动点P在x轴上移动,当△PAE是直角三角形时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【知识背景】在学习计算框图时,可以用“ ![]() ”表示数据输入、输出框;用“
”表示数据输入、输出框;用“ ![]() ”表示数据处理和运算框;用“
”表示数据处理和运算框;用“ ![]() ”表示数据判断框(根据条件决定执行两条路径中的某一条)
”表示数据判断框(根据条件决定执行两条路径中的某一条) 
(1)【尝试解决】 ①如图1,当输入数x=﹣2时,输出数y=
②如图2,第一个“ ![]() ”内,应填; 第二个“
”内,应填; 第二个“ ![]() ”内,应填;
”内,应填;
(2)①如图3,当输入数x=﹣1时,输出数y=; ②如图4,当输出的值y=17,则输入的值x=
(3)【实际应用】 为鼓励节约用水,决定对用水实行“阶梯价”:当每月用水量不超过10吨时(含10吨),以3元/吨的价格收费;当每月用水量超过10吨时,超过部分以4元/吨的价格收费.请设计出一个“计算框图”,使得输入数为用水量x,输出数为水费y.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com