练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在△ABC中，AB=7，AC=5，BC=6，∠ABC和∠ACB的平分线相交于点D，过点D作BC的平行线交AB于点E，交AC于点F．则△AEF的周长为（ ）

    A.9 B.11 C.12 D.13

    【答案】C

    【解析】

    试题分析：根据∠ABC和∠ACB的平分线相交于点D，过点D作BC的平行线交AB于点E，求证∠EDB=∠EBD，可得BE=ED，DF=FC，然后利用AB+AC即可求出△AEF的周长．

    解：∵BD是∠ABC的平分线，

    ∴∠EBD=∠DBC，

    ∵过点D作BC的平行线交AB于点E，

    ∴∠EDB=∠EBD，

    ∴BE=ED，

    ∴∠EDB=∠EBD，

    同理可得DF=FC，

    ∴△AEF的周长即为AB+AC=7+5=12．

    故选C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】下列运算正确的是（　　）

    A.a3（﹣b）5＝a3b5B.（﹣2a2）3＝﹣2a6

    C.2a2b2﹣ab＝2abD.﹣2ab﹣ab＝﹣3ab

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若a的相反数是﹣3，b的绝对值是4，且|b|=﹣b，则a﹣b=_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，过∠AOB的平分线上一点C作CD∥OB交OA于点D，E是线段OC的中点，过点E作直线分别交射线CD，OB于点M，N，探究线段OD，ON，DM之间的数量关系，并证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在△ABC中，AB=AC，点F是BC延长线上一点，以CF为边，作菱形CDEF，使菱形CDEF与点A在BC的同侧，连接BE，点G是BE的中点，连接AG、DG．

    （1）如图①，当∠BAC=∠DCF=90°时，直接写出AG与DG的位置和数量关系；

    （2）如图②，当∠BAC=∠DCF=60°时，试探究AG与DG的位置和数量关系，

    （3）当∠BAC=∠DCF=α时，直接写出AG与DG的数量关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】数学张老师在课堂上提出一个问题：“通过探究知道： ≈1.414…，它是个无限不循环小数，也叫无理数，它的整数部分是1，那么有谁能说出它的小数部分是多少”，小明举手回答：它的小数部分我们无法全部写出来，但可以用 ﹣1来表示它的小数部分，张老师夸奖小明真聪明，肯定了他的说法．现请你根据小明的说法解答： 已知8+ =x+y，其中x是一个整数，0＜y＜1，求2x+（y﹣ ）2016的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算(x2－3x＋n)(x2＋mx＋8)的结果中不含x2和x3的项，则m，n的值为(　　)

    A. m＝3，n＝1 B. m＝0，n＝0 C. m＝－3，n＝－9 D. m＝－3，n＝8

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列命题中是真命题的是（　　）

    A. 确定性事件发生的概率为1；

    B. 平分弦的直径垂直于弦；

    C. 正n边形都是轴对称图形,并且有n条对称轴；

    D. 两边及其一边的对角对应相等的两个三角形全等。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

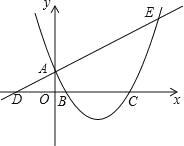
    【题目】如图，已知直线y=x+1与y轴交于点A，与x轴交于点D，抛物线y=x2+bx+c与直线交于A、E两点，与x轴交于B、C两点，且B点坐标为（1，0）．

    （1）求该抛物线的解析式；

    （2）在抛物线的对称轴上找一点M，使|AM﹣MC|的值最大，求出点M的坐标；

    （3）动点P在x轴上移动，当△PAE是直角三角形时，求点P的坐标．

    查看答案和解析>>

    同步练习册答案