
 如图,已知四边形ABCD为⊙O的内接四边形,AE是⊙O的直径,连接BE、BD,P为⊙O外一点,连接PA,若∠AEB=40°,AE=12.
如图,已知四边形ABCD为⊙O的内接四边形,AE是⊙O的直径,连接BE、BD,P为⊙O外一点,连接PA,若∠AEB=40°,AE=12.分析 (1)根据圆周角定理得到∠PAB=∠AEB,∠ABE=90°,根据余角的性质得到PA⊥AE,由切线的性质即刻得到结论;
(2)根据圆周角定理得到∠ADB=∠AEB=40°,由圆内接四边形的性质即刻得到结论.
解答 (1)证明:∵∠AEB=∠ADB,∠PAB=∠ADB,
∴∠PAB=∠AEB,
∵AE是⊙O的直径,
∴∠ABE=90°,
∴∠AEB+∠BAE=90°,
∴∠PAB+∠BAE=90°,
∴PA⊥AE,
∴PA为⊙O的切线;
(2)解:∵∠ADB=∠AEB=40°,
∵∠BDC=20°,
∴∠ADC=60°,
∵四边形ABCD为⊙O的内接四边形,
∴∠ABC=180°-∠ADC=120°.
点评 本题考查了切线的判定,圆内接四边形的性质,圆周角定理,正确的识别图形是解题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
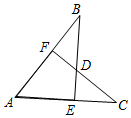 如图,AB=AC,CF⊥AB于F,BE⊥AC于E,CF与BE交于点D.有下列结论:①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上.以上结论正确的有①②③.
如图,AB=AC,CF⊥AB于F,BE⊥AC于E,CF与BE交于点D.有下列结论:①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上.以上结论正确的有①②③.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 实验的稻种数n∕粒 | 800 | 800 | 800 | 800 | 800 |
| 发芽的稻种数m∕粒 | 763 | 757 | 761 | 760 | 758 |
| 发芽的频率$\frac{m}{n}$ | 0.954 | 0.946 | 0.951 | 0.950 | 0.948 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com