
【题目】我们定义:如果一个三角形一条边上的高等于这条边,那么这个三角形叫做“等高底”三角形,这条边叫做这个三角形的“等底”.

(1)概念理解:
如图1,在△ABC中,AC=6,BC=3,∠ACB=30°,试判断△ABC是否是”等高底”三角形,请说明理由.
(2)问题探究:
如图2,△ABC是“等高底”三角形,BC是”等底”,作△ABC关于BC所在直线的对称图形得到△A'BC,连结AA′交直线BC于点D.若点B是△AA′C的重心,求![]() 的值.
的值.
(3)应用拓展:
如图3,已知l1∥l2,l1与l2之间的距离为2.“等高底”△ABC的“等底”BC在直线l1上,点A在直线l2上,有一边的长是BC的![]() 倍.将△ABC绕点C按顺时针方向旋转45°得到△A'B'C,A′C所在直线交l2于点D.求CD的值.
倍.将△ABC绕点C按顺时针方向旋转45°得到△A'B'C,A′C所在直线交l2于点D.求CD的值.
【答案】(1)△ABC是“等高底”三角形;(2)![]() ;(3)CD的值为
;(3)CD的值为![]() ,2
,2![]() ,2.
,2.
【解析】
(1)过A作AD⊥BC于D,则△ADC是直角三角形,∠ADC=90°,根据30°所对的直角边等于斜边的一半可得:![]() 根据“等高底”三角形的概念即可判断.
根据“等高底”三角形的概念即可判断.
(2)点B是![]() 的重心,得到
的重心,得到![]() 设
设![]() 则
则![]()
根据勾股定理可得![]() 即可求出它们的比值.
即可求出它们的比值.
(3)分两种情况进行讨论:①当![]() 时和②当
时和②当![]() 时.
时.
(1)△ABC是“等高底”三角形;
理由:如图1,过A作AD⊥BC于D,则△ADC是直角三角形,∠ADC=90°,
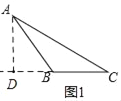
∵∠ACB=30°,AC=6,
∴![]()
∴AD=BC=3,
即△ABC是“等高底”三角形;
(2)如图2,∵△ABC是“等高底”三角形,BC是“等底”,
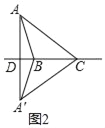
∴![]()
∵△ABC关于BC所在直线的对称图形是![]() ,
,
∴∠ADC=90°,
∵点B是![]() 的重心,
的重心,
∴![]()
设![]() 则
则![]()
由勾股定理得![]()
∴![]()
(3)①当![]() 时,
时,
Ⅰ.如图3,作AE⊥BC于E,DF⊥AC于F,
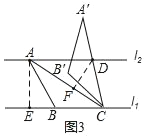
∵“等高底”△ABC的“等底”为BC,l1∥l2,l1与l2之间的距离为2,![]() .
.
∴![]()
∴BE=2,即EC=4,
∴![]()
∵△ABC绕点C按顺时针方向旋转45°得到△A'B'C,
∴∠DCF=45°,
设![]()
∵l1∥l2,
∴![]()
∴![]() 即
即![]()
∴![]()
∴![]()
Ⅱ.如图4,此时△ABC等腰直角三角形,
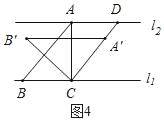
∵△ABC绕点C按顺时针方向旋转45°得到![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]()
②当![]() 时,
时,
Ⅰ.如图5,此时△ABC是等腰直角三角形,
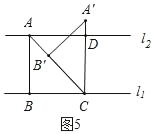
∵△ABC绕点C按顺时针方向旋转45°得到△A'B'C,
∴![]()
∴![]()
Ⅱ.如图6,作![]() 于E,则
于E,则![]()
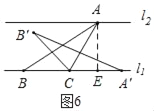
∴![]()
∴![]()
∴△ABC绕点C按顺时针方向旋转45°,得到![]() 时,点A'在直线l1上,
时,点A'在直线l1上,
∴![]() ∥l2,即直线
∥l2,即直线![]() 与l2无交点,
与l2无交点,
综上所述,CD的值为![]()


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:
【题目】如图,已知点A(1,a)是反比例函数![]() 的图象上一点,直线
的图象上一点,直线![]() 与反比例函数
与反比例函数![]() 的图象的交点为点B、D,且B(3,﹣1),求:
的图象的交点为点B、D,且B(3,﹣1),求:
(1)求反比例函数的解析式;
(2)求点D坐标,并直接写出y1>y2时x的取值范围;
(3)动点P(x,0)在x轴的正半轴上运动,当线段PA与线段PB之差达到最大时,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班“数学兴趣小组”对函数y=![]() +x的图象与性质进行了探究,探究过程如下,请补充完整.
+x的图象与性质进行了探究,探究过程如下,请补充完整.
(1)函数y=![]() +x的自变量x的取值范围是 ;
+x的自变量x的取值范围是 ;
(2)下表是y与x的几组对应值.
x | … | ﹣3 | ﹣2 | ﹣1 | 0 |
|
|
|
| 2 | 3 | 4 | 5 | … |
y | … | ﹣ | ﹣ | ﹣ | ﹣1 | ﹣ | ﹣ |
|
| 3 |
| m |
| … |
求m的值;
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(4)进一步探究发现,该函数图象在第一象限内的最低点的坐标是(2,3),结合函数的图象,写出该函数的其它性质(一条即可): .
(5)小明发现,①该函数的图象关于点( , )成中心对称;
②该函数的图象与一条垂直于x轴的直线无交点,则这条直线为 ;
③直线y=m与该函数的图象无交点,则m的取值范围为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,AB>BC,点D在边BC上,CD=2BD,点E、F在线段AD上,∠1=∠2=∠BAC,若△ABC的面积为18,则△ABE与△CDF的面积之和是( )

A.6B.8C.9D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆慢车从甲地匀速行驶至乙地,一辆快车同时从乙地出发匀速行驶至甲地,两车之间的距离y(千米)与行驶时间x(小时)的对应关系如图所示:下列结论:①甲乙两地相距600 千米;②慢车的速度是60千米/小时;③两车相距300千米时,x=2;④慢车走400千米时快车已到达甲地.其中正确的是___________________ .(填写所有正确结论的序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,点P是BC边上一动点(不与点B、C重合),连接AP,作射线PD,使∠APD=60°,PD交AC于点D,已知AB=a,设CD=y,BP=x,则y与x函数关系的大致图象是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为![]() ,连接AC、BD交于点O,CE平分∠ACD交BD于点E,
,连接AC、BD交于点O,CE平分∠ACD交BD于点E,
(1)求DE的长;
(2)过点EF作EF⊥CE,交AB于点F,求BF的长;
(3)过点E作EG⊥CE,交CD于点G,求DG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是反比例函数y=![]() (x>0)图象上一点,直线y=kx+b过点A并且与两坐标轴分别交于点B,C,过点A作AD⊥x轴,垂足为D,连接DC,若△BOC的面积是4,则△DOC的面积是______.
(x>0)图象上一点,直线y=kx+b过点A并且与两坐标轴分别交于点B,C,过点A作AD⊥x轴,垂足为D,连接DC,若△BOC的面积是4,则△DOC的面积是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙三个盒子中分别装有除颜色外都相同的小球,甲盒中装有两个球,分别为一个红球和一个绿球;乙盒中装有三个球,分别为两个绿球和一个红球;丙盒中装有两个球,分别为一个红球和一个绿球,从三个盒子中各随机取出一个小球
(1)请画树状图,列举所有可能出现的结果
(2)请直接写出事件“取出至少一个红球”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com