
分析 把m代入已知方程并求得m的值;然后把它代入所求的代数式进行求值.
解答 解:依题意得:m-$\sqrt{3}$=0,
解得m=$\sqrt{3}$,
则(m2-1)(m-$\frac{m}{3}$+1)=[($\sqrt{3}$)2-1]($\sqrt{3}$-$\frac{\sqrt{3}}{3}$+1)=2×$\frac{2\sqrt{3}+3}{3}$=$\frac{4\sqrt{3}+6}{3}$,即(m2-1)(m-$\frac{m}{3}$+1)=$\frac{4\sqrt{3}+6}{3}$.
点评 本题考查了二次根式的化简求值.根据一元一次方程的解的定义求得m的值是解题的关键.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:解答题
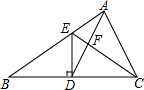 如图,在△ABC中,D是BC边上的中点,AD=AC,DE⊥BC,交AB于点E,CE与AD相交于点F,BC=10,S△CDF=6.
如图,在△ABC中,D是BC边上的中点,AD=AC,DE⊥BC,交AB于点E,CE与AD相交于点F,BC=10,S△CDF=6.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
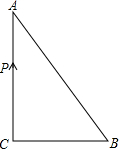 如图,在Rt△ABC中,∠C=90°,BC=6cm,CA=8cm,动点P从点C出发,以2cm/s的速度沿CA、AB移动到B,则点P出发( )时,可使S△BCP=$\frac{1}{4}$S△ABC.
如图,在Rt△ABC中,∠C=90°,BC=6cm,CA=8cm,动点P从点C出发,以2cm/s的速度沿CA、AB移动到B,则点P出发( )时,可使S△BCP=$\frac{1}{4}$S△ABC.| A. | 1s | B. | $\frac{31}{4}$s | C. | 1s或$\frac{31}{4}$s | D. | 2s |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
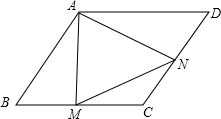 如图,已知菱形ABCD中,∠BAD=120°,M为BC上一点,N为CD上一点,求证:若△AMN有一个内角等于60°,则△AMN为等边三角形.
如图,已知菱形ABCD中,∠BAD=120°,M为BC上一点,N为CD上一点,求证:若△AMN有一个内角等于60°,则△AMN为等边三角形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com