
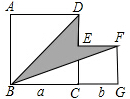
 如图,两个正方形的边长分别为acm,bcm(a>b),若a+b=5cm,ab=3cm,求图中阴影部分的面积.
如图,两个正方形的边长分别为acm,bcm(a>b),若a+b=5cm,ab=3cm,求图中阴影部分的面积. 分析 根据题意,连接BE,将图中阴影部分的面积转化为求△DEB和△EFB的面积,从而可以解答本题.
解答 解:如下图所示: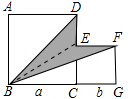
连接BE,
∵两个正方形的边长分别为acm,bcm(a>b),
∴图中阴影部分的面积为:S△BED+S△BEF=$\frac{DE×BC}{2}+\frac{EF×GF}{2}$=$\frac{(a-b)×a}{2}+\frac{b×b}{2}=\frac{{a}^{2}-ab+{b}^{2}}{2}$=$\frac{(a+b)^{2}-3ab}{2}$.
∵a+b=5cm,ab=3cm,
∴$\frac{(a+b)^{2}-3ab}{2}=\frac{{5}^{2}-3×3}{2}=\frac{16}{2}=8$cm2.
即图中阴影部分的面积是8cm2.
点评 本题考查列代数式和代数式的求值、三角形的面积,解题的关键是运用转化的数学思想,将阴影部分的面积转化为求△DEB和△EFB的面积.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
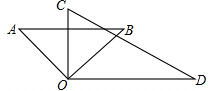 如图所示,小红将两个直角三角形AOB,COD摆放在桌面上,使得它们的直角顶点重合在一起,小红得到出两个结论:(1)∠AOC=∠BOD;(2)∠AOD与∠BOC互补,请你判断她得出的两个结论是否正确,并说明理由.
如图所示,小红将两个直角三角形AOB,COD摆放在桌面上,使得它们的直角顶点重合在一起,小红得到出两个结论:(1)∠AOC=∠BOD;(2)∠AOD与∠BOC互补,请你判断她得出的两个结论是否正确,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com