【题目】在
中，
于
，
是
的平分线，
，
，求
和
的度数．
【答案】30°；20°；
【解析】
由CD⊥AB与∠B=60°，根据两锐角互余，即可求得∠BCD的度数；由∠A=20°，∠B=60°，求得∠ACB的度数，由CE是∠ACB的平分线，可求得∠ACE的度数，然后根据三角形外角的性质，求得∠CEB的度数，继而可得．
(1)∵CD⊥AB，
∴∠CDB=90°，
∵∠B=60°，
∴∠BCD=90°∠B=90°60°=30°；
∵∠A=20°,∠B=60°,∠A+∠B+∠ACB=180°，
∴∠ACB=100°，
∵CE是∠ACB的平分线，
∴∠ACE=
∠ACB=50°，
∴∠CEB=∠A+∠ACE=20°+50°=70°，
∠ECD=90°70°=20°.
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目：初中数学 来源： 题型：
【题目】如图1，正方形ABCD的边长为6cm，点F从点B出发，沿射线AB方向以1cm/秒的速度移动，点E从点D出发，向点A以1cm/秒的速度移动（不到点A）．设点E，F同时出发移动t秒．
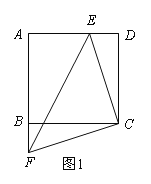
（1）在点E，F移动过程中，连接CE，CF，EF，则△CEF的形状是 ，始终保持不变；
（2）如图2，连接EF，设EF交BD于点M，当t=2时，求AM的长；
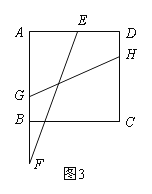
（3）如图3，点G，H分别在边AB，CD上，且GH=
cm，连接EF，当EF与GH的夹角为45°，求t的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读材料并回答问题：
我们知道，乘法公式可以用平面几何图形的面积来表示，实际上还有一些代数恒等式也可以用这种形式表示，如：
，就可以用图1或图2等图形的面积表示．
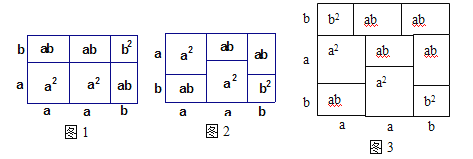
（1）请写出图3所表示的代数恒等式： ；
（2）试画一个几何图形，使它的面积表示：
；
（3）请仿照上述方法另写一个含有
，
的代数恒等式，并画出与它对应的几何图形．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，一次函数y＝kx+b(k，b为常数，k≠0)的图象与反比例函数
的图象交于A、B两点，且与x轴交于点C，与y轴交于点D，A点的横坐标与B点的纵坐标都是3.
(1)求一次函数的表达式；
(2)求△AOB的面积；
(3)写出不等式kx+b＞﹣
的解集.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，Rt△ABC中，∠ACB＝90°，BC＝AC＝3，点D是BC边上一点，∠DAC＝30°，点E是AD边上一点，CE绕点C逆时针旋转90°得到CF，连接DF，DF的最小值是___．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在如图所示的正方形网格中，每个小正方形的边长为1，格点三角形（顶点是网格线的交点的三角形）
在如图所示的位置．
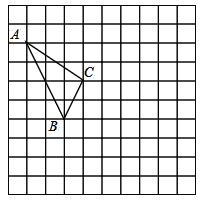
（1）将
向右平移4个单位，向下平移3个单位得△
，请在网格中作出△；
（2）若连接
，
，则这两条线段的位置关系是 ；
（3）的面积为 ；
（4）在整个平移过程中，
点的运动路径长为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图是二次函数y=ax2+bx+c的图象的一部分，对称轴是直线x=1．
①b2＞4ac； ②4a-2b+c＜0； ③不等式ax2+bx+c＞0的解集是x≥3.5； ④若（-2，y1），（5，y2）是抛物线上的两点，则y1＜y2．
上述4个判断中，正确的是（ ）
A. ①② B. ①④ C. ①③④ D. ②③④
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，动点
在平面直角坐标系中按图中箭头所示方向运动，第
次从原点运动到点
，第
次接着运动到点
，第
次接着运动到点
，
按这样的运动规律，经过第
次运动后，动点的坐标是（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
