
【题目】如图,在平面直角坐标系中,等腰Rt△AOB的斜边OB在x轴上,直线y=3x-4经过等腰Rt△AOB的直角顶点A,交y轴于C点,双曲线y=![]() 也经过A点.
也经过A点.
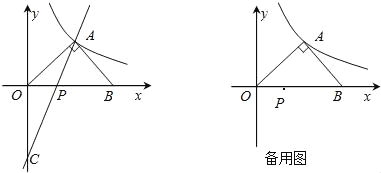
(1)求点A的坐标和k的值;
(2)若点P为x轴上一动点.在双曲线上是否存在一点Q,使得△PAQ是以点A为直角顶点的等腰三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
【答案】(1)点A的坐标为(2,2),k=4;(2) 在双曲线上存在一点Q(4,1),使得△PAQ是以点A为直角顶点的等腰三角形.
【解析】
试题分析:(1)过点A分别作AM⊥y轴于M点,AN⊥x轴于N点,根据直角三角形的性质可设点A的坐标为(a,a),因为点A在直线y=3x-4上,即把A点坐标代入解析式即可算出a的值,进而得到A点坐标,然后再利用待定系数法求出反比例函数解析式;
(2)如果过B作BQ⊥x轴交双曲线于Q点,连接AQ,过A点作AP⊥AQ交x轴于P点.由ASA易证△AOP≌△ABQ,得出AP=AQ,那么△APQ是所求的等腰直角三角形.根据全等三角形的性质及函数图象与点的坐标的关系得出结果.
试题解析:(1)过点A分别作AM⊥y轴于M点,AN⊥x轴于N点,
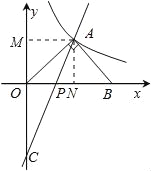
∵△AOB是等腰直角三角形,
∴AM=AN.
设点A的坐标为(a,a),
∵点A在直线y=3x-4上,
∴a=3a-4,
解得a=2,
则点A的坐标为(2,2),
∵双曲线y=![]() 也经过A点,
也经过A点,
∴k=4;
(2)假设双曲线上存在一点Q,使得△PAQ是等腰直角三角形.
过B作BQ⊥x轴交双曲线于Q点,连接AQ,过A点作AP⊥AQ交x轴于P点,
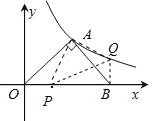
则△APQ为所求作的等腰直角三角形.
理由:在△AOP与△ABQ中,
∵∠OAB-∠PAB=∠PAQ-∠PAB,
∴∠OAP=∠BAQ,
在△AOP和△ABQ中
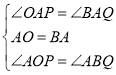 ,
,
∴△AOP≌△ABQ(ASA),
∴AP=AQ,
∴△APQ是所求的等腰直角三角形.
∵B(4,0),
∴Q(4,1),
经检验,在双曲线上存在一点Q(4,1),使得△PAQ是以点A为直角顶点的等腰三角形.


科目:初中数学 来源: 题型:
【题目】已知:如下图, AB∥CD,点E,F分别为AB,CD上一点.
(1) 在AB,CD之间有一点M(点M不在线段EF上),连接ME,MF,试探究∠AEM,∠EMF,∠MFC之间有怎样的数量关系. 请补全图形,并在图形下面写出相应的数量关系,选其中一个进行证明.

(2)如下图,在AB,CD之间有两点M,N,连接ME,MN,NF,请选择一个图形写出∠AEM,∠EMN,∠MNF,∠NFC 存在的数量关系(不需证明).
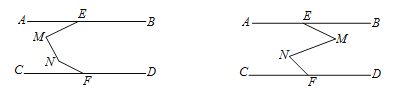
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)某商场用2500元购进了A、B两种新型节能台灯共50盏,这两种台灯的进价,标价如下表所示:

(1)这两种台灯各购进多少盏?
(2)若A型台灯按标价的九折出售,B型台灯按标价的八折出售,那么这批台灯全部售完后,商场共获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下三条线段为边,能组成三角形的是( )
A.1cm、2cm、3cm
B.2cm、2cm、4cm
C.3cm、4cm、5 cm
D.4cm、8cm、2cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1)所示,E为矩形ABCD的边AD上一点,动点P、Q同时从点B出发,点P沿折线BE-ED-DC运动到点C时停止,点Q沿BC运动到点C时停止,它们运动的速度都是1cm/秒.设P、Q同发t秒时,△BPQ的面积为ycm2.已知y与t的函数关系图象如图(2)(曲线OM为抛物线的一部分),则下列结论:

①AD=BE=5;
②cos∠ABE=![]() ;
;
③当0<t≤5时,y=![]() t2;
t2;
④当t=![]() 秒时,△ABE∽△QBP;
秒时,△ABE∽△QBP;
其中正确的结论是 (填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ACD和△BCE都是等腰直角三角形,∠ACD=∠BCE=90°,AE交DC于F,BD分别交CE、AE于点G、H.试猜测线段AE和BD的位置和数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年我省粮食总产量695.2亿斤,居历史第二高位,695.2亿用科学记数法表示为:
A. 695.2×108 B. 6.952×109 C. 6.952×1010 D. 6.952×1011
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com