
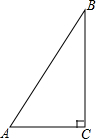
 如图,在△ABC中,∠C=90°,sinA=$\frac{4}{5}$,AB=10,求△ABC的周长和tanA的值.
如图,在△ABC中,∠C=90°,sinA=$\frac{4}{5}$,AB=10,求△ABC的周长和tanA的值. 分析 根据题中所给的条件,在直角三角形中解题,根据角的余弦值与三角形边的关系及勾股定理,可求出各边的长,代入三角函数进行求解.
解答 解:在Rt△ABC中,∠C=90°,AB=10
sinA=$\frac{BC}{AB}$=$\frac{4}{5}$,
∴BC=8,
AC=$\sqrt{A{B}^{2}-B{C}^{2}}=8$,
∴△ABC的周长=AB+AC+BC=24,
tanA=$\frac{BC}{AC}$=$\frac{4}{3}$.
点评 本题考查了利用锐角三角函数和勾股定理解直角三角形的能力,还考查解直角三角形的定义,由直角三角形已知元素求未知元素的过程,还考查了直角三角形的性质.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
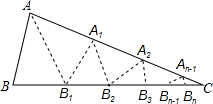 如图,△ABC中,沿∠BAC的平分线AB.折叠,剪掉重叠部分;将余下部分沿∠B1A1C的平分线A1B2折叠,剪掉重叠部分,…;将余下部分沿∠An-1Bn-1折叠,经过n次折叠,若点Bn-1于点C重合,就称∠ABC的n阶“完美”角.
如图,△ABC中,沿∠BAC的平分线AB.折叠,剪掉重叠部分;将余下部分沿∠B1A1C的平分线A1B2折叠,剪掉重叠部分,…;将余下部分沿∠An-1Bn-1折叠,经过n次折叠,若点Bn-1于点C重合,就称∠ABC的n阶“完美”角.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 220千米 | B. | 240千米 | C. | 260千米 | D. | 350千米 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com