
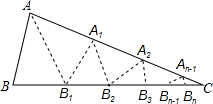
 如图,△ABC中,沿∠BAC的平分线AB.折叠,剪掉重叠部分;将余下部分沿∠B1A1C的平分线A1B2折叠,剪掉重叠部分,…;将余下部分沿∠An-1Bn-1折叠,经过n次折叠,若点Bn-1于点C重合,就称∠ABC的n阶“完美”角.
如图,△ABC中,沿∠BAC的平分线AB.折叠,剪掉重叠部分;将余下部分沿∠B1A1C的平分线A1B2折叠,剪掉重叠部分,…;将余下部分沿∠An-1Bn-1折叠,经过n次折叠,若点Bn-1于点C重合,就称∠ABC的n阶“完美”角.分析 (1)根据题意∠B=90°,∠C=30°,∠BAC=60°,设B1B2=B2A2=A2C=a,则CM=MB2=$\frac{\sqrt{3}}{2}$x,列出方程即可解决.
(2)假设∠A是2阶“完美”角,∠A>∠C≥∠B,由题意设∠B=y,∠C=ny,∠A=2ny(n为正整数),根据内角和定理,以及∠A,∠B,∠C都是整数,可以得到n=1或3由此即可解决问题.
解答 解:(1)如图1中,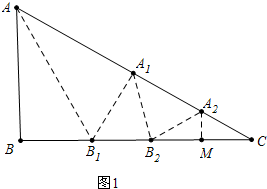 AM为折痕,
AM为折痕,
∵A2M⊥BC,AB∥A2M,
∴∠B=90°,设∠C=x,则∠A2B2C=x,∠A1A2B2=∠A1B1C=2x,
∴∠AA1B1=∠B=∠A1B1C+∠C,
∴3x=90°,
∴x=30°,
∴∠C=30°,∠BAC=60°,
在RT△ABB1中,∵∠BAB1=30°,AB=3,
∴BB1=$\sqrt{3}$,又BC=3$\sqrt{3}$,
∴B1C=2$\sqrt{3}$,设B1B2=B2A2=A2C=a,则CM=MB2=$\frac{\sqrt{3}}{2}$x,
∴x+$\sqrt{3}$x=2$\sqrt{3}$,
x=3-$\sqrt{3}$.
(2)假设∠A是2阶“完美”角,∠A>∠C≥∠B,由题意设∠B=y,∠C=ny,∠A=2ny(n为正整数),
∵y+ny+2ny=180°,
∴y=$\frac{180°}{3n+1}$,
∵$\frac{180°}{3n+1}$>10°
∴n<$\frac{17}{3}$,
∵n为正整数,
∴n=1或2或3或4或5,
∵∠A,∠B,∠C都是整数,
∴n=1或3,
∴三角形的三个内角分别为45°,45°,90°或18°,54°,108°.
点评 本题考查翻折不变性,理解题意是解决问题的关键,学会利用不等式,把问题转化为求不等式的整数解,难度比较大,考查学生综合利用知识的能力.


科目:初中数学 来源: 题型:填空题
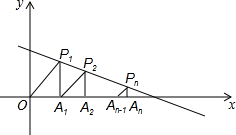 如图所示,在函数y=-$\frac{1}{3}$x+$\frac{4}{3}$(x>0)的图象上,△P1OA,△P2A1A2,△P2A2A3,…,△PnAn-1An都是等腰直角三角形,且直角边OA1,A1A2,…,An-1An都在x轴上,则An的坐标为Pn[1+$\frac{3}{4}$+$\frac{9}{16}$+…($\frac{3}{4}$)n-1,($\frac{3}{4}$)n-1].
如图所示,在函数y=-$\frac{1}{3}$x+$\frac{4}{3}$(x>0)的图象上,△P1OA,△P2A1A2,△P2A2A3,…,△PnAn-1An都是等腰直角三角形,且直角边OA1,A1A2,…,An-1An都在x轴上,则An的坐标为Pn[1+$\frac{3}{4}$+$\frac{9}{16}$+…($\frac{3}{4}$)n-1,($\frac{3}{4}$)n-1].查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
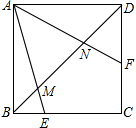 如图,正方形ABCD中,点E、F分别是BC、CD边上的点,且∠EAF=45°,对角线BD交AE于点M,交AF于点N.若AB=4$\sqrt{2}$,BM=2,则MN的长为$\frac{10}{3}$.
如图,正方形ABCD中,点E、F分别是BC、CD边上的点,且∠EAF=45°,对角线BD交AE于点M,交AF于点N.若AB=4$\sqrt{2}$,BM=2,则MN的长为$\frac{10}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
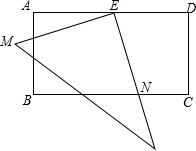 在长方形ABCD中,AD=2AB,E是AD的中点,一块三角板的直角顶点与点E重合,将三角板绕点E按顺时针方向旋转,当三角板的两直角边分别与AB、BC分别相交于点M,N时,观察或测量BM与CN的长度,你能得到什么结论?并证明你的结论.
在长方形ABCD中,AD=2AB,E是AD的中点,一块三角板的直角顶点与点E重合,将三角板绕点E按顺时针方向旋转,当三角板的两直角边分别与AB、BC分别相交于点M,N时,观察或测量BM与CN的长度,你能得到什么结论?并证明你的结论.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com