

分析 (1)如图1中,作AM⊥CF于M,由△ACM≌△CBO,得CM=BO=4即可解决.
(2)求出线段BC,BF,AF,AE,得出$\frac{AF}{BF}=\frac{AE}{BC}$,可以证△AEF∽△BCF得到∠AEF=∠BCF,再证明∠BCF=∠OEC即可.
(3)如图2中,作AM⊥OC于M,只要证明△ACM≌△CBO得CM=BO,由四边形ADOM是矩形得AD=OM,即可得出CO-AD=CO-OM=CM=BO,即可解决问题.
解答 (1)解:如图1中,作AM⊥CF于M.
∵∠ACM+∠BCO=90°,∠BCO+∠CBO=90°,
∴∠ACM=∠CBO,
在△ACM和△CBO中,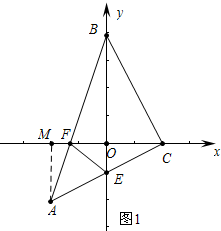
$\left\{\begin{array}{l}{∠AMC=∠BOC=90°}\\{∠ACM=∠CBO}\\{AC=BC}\end{array}\right.$,
∴△ACM≌△CBO,
∴CM=BO=4,
∴点B坐标(0,4).
(2)如图2中,∵AM∥BO,AM=MO=2,
∴$\frac{AM}{BO}=\frac{MF}{FO}$=$\frac{1}{2}$,
∴MF=$\frac{2}{3}$,FO=$\frac{4}{3}$,AF=$\sqrt{A{M}^{2}+F{M}^{2}}$=$\frac{2\sqrt{10}}{3}$,
∵OE∥MA,OM=0C=2,
∴AE=EC=$\frac{1}{2}$AC①得证,
∵AC=$\sqrt{A{M}^{2}+C{M}^{2}}$=2$\sqrt{5}$,AB=$\sqrt{{2}^{2}+{6}^{2}}$=2$\sqrt{10}$,BC=2$\sqrt{5}$
∴AE=$\sqrt{5}$,BF=$\frac{4\sqrt{10}}{3}$,
∴$\frac{AF}{BF}=\frac{1}{2}$,$\frac{AE}{BC}$=$\frac{1}{2}$,
∴$\frac{AF}{BF}=\frac{AE}{BC}$,
∵∠EAF=∠CBF,
∴△AEF∽△BCF,
∴∠AEF=∠BCF,
∵∠BCF+∠OCE=90°,∠OCE+∠OEC=90°,
∴∠BCF=∠OEC=∠AEF,
∴∠CEB=∠AEF②得证.
(3)如图2中,作AM⊥OC于M,
∵∠ACM+∠BCO=90°,∠ACM+∠MAC=90°,
∴∠MAC=∠BCO,
在△ACM和△CBO中,
$\left\{\begin{array}{l}{∠MAC=∠BCO}\\{∠AMC=∠BOC=90°}\\{AC=CB}\end{array}\right.$,
∴△ACM≌△CBO,
∴CM=BO,
∵∠ADO=∠DOM=∠AMO=90°,
∴四边形ADOM是矩形,
∴AD=OM,
∴$\frac{CO-AD}{OB}$=$\frac{CO-OM}{BO}$=$\frac{BO}{BO}$=1.
点评 本题考查全等三角形的判定和性质、等腰直角三角形的性质、相似三角形的判定等知识,解题的关键的第二个问题利用两边成比例夹角相等两个三角形相似,解决了角相等问题,题目难度比较大,属于中考压轴题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
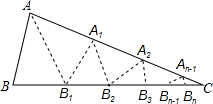 如图,△ABC中,沿∠BAC的平分线AB.折叠,剪掉重叠部分;将余下部分沿∠B1A1C的平分线A1B2折叠,剪掉重叠部分,…;将余下部分沿∠An-1Bn-1折叠,经过n次折叠,若点Bn-1于点C重合,就称∠ABC的n阶“完美”角.
如图,△ABC中,沿∠BAC的平分线AB.折叠,剪掉重叠部分;将余下部分沿∠B1A1C的平分线A1B2折叠,剪掉重叠部分,…;将余下部分沿∠An-1Bn-1折叠,经过n次折叠,若点Bn-1于点C重合,就称∠ABC的n阶“完美”角.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com