
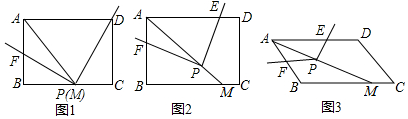
分析 (1)证得△PBF≌△DCP,再根据全等三角形的性质:对应边相等可得:PE=PF;
(2)过点P分别作AB、AD的垂线,垂足分别为G、H,有材料提供的证明思路可证明△PGF∽△PHE,再根据相似三角形的性质:对应边的比值相等可得:$\frac{PF}{PE}$=$\frac{n}{m}$;
(3)过点P作PG∥BC,作PK∥CD交AD于K,作∠GPH=∠EPF,交AD于H,由(2)的思路可证明△PGF∽△PHE,再根据相似三角形的性质:对应边的比值相等可得:$\frac{PF}{PE}$=$\frac{PG}{PH}$,然后再证得四边形AGPK是平行四边形,△KPH是等腰三角形,即可证得$\frac{PF}{PE}$=$\frac{PG}{PH}$=$\frac{PG}{AG}$=$\frac{n}{m}$.
解答 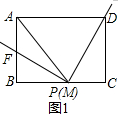 (1)证明:如图1,∵∠DPF=90°,
(1)证明:如图1,∵∠DPF=90°,
∴∠BPF+∠DPC=90°,
∵∠BFP+∠BPF=90°,
∴∠BFP=∠CPD,
∵$\frac{AB}{BM}$=1,
∴AB=BP=CD,
在△PBF和△DCP中
$\left\{\begin{array}{l}{∠BFP=∠CPD}\\{∠B=∠C=90°}\\{BP=CD}\end{array}\right.$
∴△PBF≌△DCP(AAS),
∴PF=PD;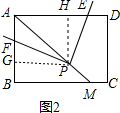
(2)解:过点P分别作AB、AD的垂线,垂足分别为G、H,如图2,
∵AB⊥AD,
∴四边形AGPH是矩形,
∴AG=PH,∠GPH=90°
∵PO∥BC,
∴△AGP∽△ABM,
∴$\frac{AG}{PG}$=$\frac{AB}{BM}$=$\frac{m}{n}$,
∵∠EPF=90°,
∴∠GPH-∠FPH=∠EPF-∠FPH,即∠GPF=∠HPE,
∵∠PGF=∠PHE=90°,
∴△PGF∽△PHE,
∴$\frac{PF}{PE}$=$\frac{PG}{PH}$=$\frac{PG}{AG}$=$\frac{n}{m}$;
(3)解:成立,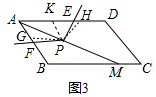
过点P作PG∥BC,作∠GPH=∠EPF,交AD于H,如图3,
∴∠GPH-∠GPE=∠EPF-∠GPE,即∠FPG=∠EPH,
∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,∠BAD+∠D=180°,
∵FPE=∠D,
∴∠BAD+∠FPE=180°,
∴∠PFA+∠PEA=180°,
∵∠PEA+∠PEH=180°,
∴∠PFG=∠PEH,
∴△FPG∽△EPH,
∴$\frac{PF}{PE}$=$\frac{PG}{PH}$,
∵PG∥BC,
∴△APG∽△AMB,
∴$\frac{AG}{PG}$=$\frac{AB}{BM}$=$\frac{m}{n}$,
作PK∥CD交AD于K,
∴∠PKE=∠BAD,
∵∠FPG=∠EPH,∠PFG=∠PEH,
∴∠PGF=∠PHE.
∵PG∥BC∥AD,
∴∠PGF=∠BAD,
∴∠PKE=∠PHE,
∴PK=PH,
∵PG∥AD,PK∥AB,
∴四边形AGPK是平行四边形,
∴AG=PK=PH,
∴$\frac{PF}{PE}$=$\frac{PG}{PH}$=$\frac{PG}{AG}$=$\frac{n}{m}$.
点评 本题是一个动态几何题,考查了矩形性质、平行四边形的判定和性质、全等三角形的判定以及性质,三角形相似的判定和性质及等腰三角形的判定和性质,作出辅助线构建相似三角形是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
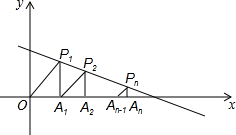 如图所示,在函数y=-$\frac{1}{3}$x+$\frac{4}{3}$(x>0)的图象上,△P1OA,△P2A1A2,△P2A2A3,…,△PnAn-1An都是等腰直角三角形,且直角边OA1,A1A2,…,An-1An都在x轴上,则An的坐标为Pn[1+$\frac{3}{4}$+$\frac{9}{16}$+…($\frac{3}{4}$)n-1,($\frac{3}{4}$)n-1].
如图所示,在函数y=-$\frac{1}{3}$x+$\frac{4}{3}$(x>0)的图象上,△P1OA,△P2A1A2,△P2A2A3,…,△PnAn-1An都是等腰直角三角形,且直角边OA1,A1A2,…,An-1An都在x轴上,则An的坐标为Pn[1+$\frac{3}{4}$+$\frac{9}{16}$+…($\frac{3}{4}$)n-1,($\frac{3}{4}$)n-1].查看答案和解析>>
科目:初中数学 来源: 题型:填空题
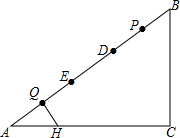 如图,在Rt△ABC中,∠C=90°,BC=6,AC=8,点P,Q都是斜边AB上的动点,点P从B向A运动(不与点B重合),点Q从A向B运动,BP=AQ.点E,D分别是点A,B以Q,P为对称中心的对称点,HQ⊥AB,垂足为点Q,交AC于点H.当点E到达顶点B时,Q,P同时停止运动,则当△HDE为等腰三角形时,BP的值为$\frac{40}{21}$或$\frac{40}{11}$或5或$\frac{320}{103}$.
如图,在Rt△ABC中,∠C=90°,BC=6,AC=8,点P,Q都是斜边AB上的动点,点P从B向A运动(不与点B重合),点Q从A向B运动,BP=AQ.点E,D分别是点A,B以Q,P为对称中心的对称点,HQ⊥AB,垂足为点Q,交AC于点H.当点E到达顶点B时,Q,P同时停止运动,则当△HDE为等腰三角形时,BP的值为$\frac{40}{21}$或$\frac{40}{11}$或5或$\frac{320}{103}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com