
分析 (1)本题可根据两车的辆数的数量关系来列方程.等量关系为:装270台需A型车的数量=装300台需B型车的数量+1.由此可得出方程求出未知数.
(2)可先根据(1)求出单独用两种车分别要多少费用,然后让同时用两种车时花的费用小于单独用一种车的最少的费用.得出车的数量的取值范围,然后判断出有几种运输方案,然后根据运输方案求出运费.
解答 解:(1)设A型汽车每辆可装计算机x台,则B型汽车每辆可装计算机(x+15)台.
依题意得:$\frac{270}{x}$=$\frac{270+30}{x+15}$+1.
解得:x=45,x=-90(舍去).
经检验:x=45是原方程的解.
则x+15=60.
答:A型汽车每辆可装计算机45台,B型汽车每辆可装计算机60台.
(2)由(1)知.
若单独用A型汽车运送,需6辆,运费为2100元;
若单独用B型汽车运送,需车5辆,运费为2000元.
若按这种方案需同时用A,B两种型号的汽车运送,设需要用A型汽车y辆,则需B型汽车(y+1)辆.根据题意可得:350y+400(y+1)<2000.
解得:y<$\frac{32}{15}$.
因汽车辆数为正整数.∴y=1或2.
当y=1时,y+1=2.则45×1+60×2=165<270.不同题意.
当y=2时,y+1=3.则45×2+60×3=270.符合题意.
此时运费为350×2+400×3=1900元.
答:需要用A型汽车2辆,则需B型汽车3辆.运费1900元
点评 本题考查了分式方程的应用.解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程或不等式,再求解.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
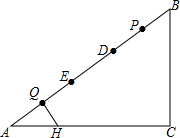 如图,在Rt△ABC中,∠C=90°,BC=6,AC=8,点P,Q都是斜边AB上的动点,点P从B向A运动(不与点B重合),点Q从A向B运动,BP=AQ.点E,D分别是点A,B以Q,P为对称中心的对称点,HQ⊥AB,垂足为点Q,交AC于点H.当点E到达顶点B时,Q,P同时停止运动,则当△HDE为等腰三角形时,BP的值为$\frac{40}{21}$或$\frac{40}{11}$或5或$\frac{320}{103}$.
如图,在Rt△ABC中,∠C=90°,BC=6,AC=8,点P,Q都是斜边AB上的动点,点P从B向A运动(不与点B重合),点Q从A向B运动,BP=AQ.点E,D分别是点A,B以Q,P为对称中心的对称点,HQ⊥AB,垂足为点Q,交AC于点H.当点E到达顶点B时,Q,P同时停止运动,则当△HDE为等腰三角形时,BP的值为$\frac{40}{21}$或$\frac{40}{11}$或5或$\frac{320}{103}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,点D,E分别是AC,AB上的两点,且$\frac{AD}{AB}$=$\frac{AE}{AC}$=$\frac{1}{2}$,若△ADE的面积为1cm2,则四边形EBCD的面积为( )cm2.
如图,在△ABC中,点D,E分别是AC,AB上的两点,且$\frac{AD}{AB}$=$\frac{AE}{AC}$=$\frac{1}{2}$,若△ADE的面积为1cm2,则四边形EBCD的面积为( )cm2.| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com