
【题目】如图,在Rt△ABC中,AB=AC,D、E是斜边BC上两动点,且∠DAE=45°,将△ABE绕点A逆时针旋转90°后,得到△AFC,连接DF.
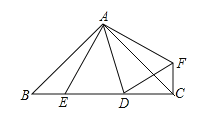
(1)试说明:△AED≌△AFD;
(2)当BE=3,CE=9时,求∠BCF的度数和DE的长;
【答案】(1)见解析;(2)90°,5.
【解析】
(1)根据旋转的性质,可得对应角与对应边相等;根据全等三角形的判定定理即可证明;
(2)设DE=x,则CD=9﹣x.在Rt△DCF中,由DF2=CD2+CF2,CF=BE=3,推出x2=(9﹣x)2+32,解方程即可.
(1)证明:∵将△ABE绕点A逆时针旋转90°后,得到△AFC,
∴△BAE≌△CAF,
∴AE=AF,∠BAE=∠CAF,BE=CF,
∵∠BAC=90°,∠EAD=45°,
∴∠CAD+∠BAE=∠CAD+∠CAF=45°,
∴∠DAE=∠DAF,
∵DA=DA,AE=AF,
∴△AED≌△AFD(SAS);
(2)解:设DE=x,则CD=9﹣x.
∵AB=AC,∠BAC=90°,
∴∠B=∠ACB=45°,
∵∠ABE=∠ACF=45°,
∴∠BCF=90°,
∵△AED≌△AFD,
∴DE=DF=x,
在Rt△DCF中,∵DF2=CD2+CF2,CF=BE=3,
∴x2=(9﹣x)2+32,
∴x=5,
∴DE=5.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,∠ACB=45°,点E在对角线AC上,BE=BA,BF⊥AC于点F,BF的延长线交AD于点G.点H在BC的延长线上,且CH=AG,连接EH.
(1)若BC=12![]() ,AB=13,求AF的长;
,AB=13,求AF的长;
(2)求证:EB=EH.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】锐锐参加我市电视台组织的“牡丹杯”智力竞答节目,答对最后两道单选题就顺利通关,第一道单选题有3个选项,第二道单选题有4个选项,这两道题锐锐都不会,不过锐锐还有两个“求助”可以用(使用“求助”一次可以让主持人去掉其中一题的一个错误选项).
(1)如果锐锐两次“求助”都在第一道题中使用,那么锐锐通关的概率是________;
(2)如果锐锐两次“求助”都在第二道题中使用,那么锐锐通关的概率是________;
(3)如果锐锐每道题各用一次“求助”,请用树状图或者列表来分析他顺利通关的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某开发区有一块四边形的空地ABCD,如图所示,现计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,问要多少投入?
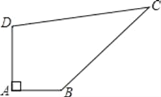
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角坐标系中,![]() 的顶点都在网格点上,其中,C点坐标为
的顶点都在网格点上,其中,C点坐标为![]() .
.
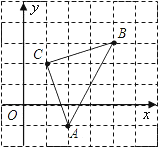
(1)写出点A、B的坐标:
![]() ______ ,______
______ ,______ ![]() 、
、![]() ______ ,______
______ ,______ ![]()
(2)将![]() 先向左平移2个单位长度,再向上平移1个单位长度,得到
先向左平移2个单位长度,再向上平移1个单位长度,得到![]() ,则
,则![]() 的三个顶点坐标分别是
的三个顶点坐标分别是![]() ______ ,______
______ ,______ ![]() 、
、![]() ______ ,______
______ ,______ ![]() 、
、![]() ______ ,______
______ ,______ ![]()
(3)求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有![]() 、
、![]() 、
、![]() 三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )
三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )

A.在∠A、∠B两内角平分线的交点处
B.在AC、BC两边垂直平分线的交点处
C.在AC、BC两边高线的交点处
D.在AC、BC两边中线的交点处
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小型企业实行工资与业绩挂钩制度,工人工资分为A、B、C、D四个档次.小明对该企业三月份工人工资进行调查,并根据收集到的数据,绘制了如下尚不完整的统计表与扇形统计图.
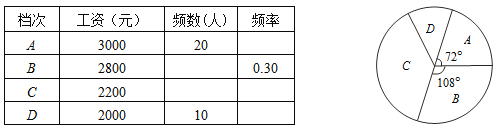
根据上面提供的信息,回答下列问题:
(1)求该企业共有多少人?
(2)请将统计表补充完整;
(3)扇形统计图中“C档次”的扇形所对的圆心角是 度.
查看答案和解析>>
科目:初中数学 来源: 题型:
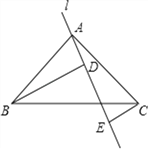
【题目】如图,Rt△ABC中,AB=AC,∠BAC=90°,直线l为经过点A的任一直线,BD⊥l于D,CE⊥AE,若BD>CE,试问:
(1)AD与CE的大小关系如何?请说明理由;
(2)线段BD,DE,CE之间的数量之间关系如何?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com