
分析 (1)根据已知得出式子变化规律写出答案即可;
(2)进而由(1)的规律得出答案;
(3)利用发现的规律化简各式进而求出即可.
解答 解:(1)$\frac{1}{\sqrt{2015}+\sqrt{2014}}$=$\sqrt{2015}$-$\sqrt{2014}$;
故答案为:$\sqrt{2015}$-$\sqrt{2014}$;
(2)$\frac{1}{\sqrt{n+1}+\sqrt{n}}$=$\sqrt{n+1}$-$\sqrt{n}$;(n为正整数);
故答案为:$\sqrt{n+1}$-$\sqrt{n}$;
(3)$\frac{1}{1+\sqrt{2}}$$+\frac{1}{\sqrt{2}+\sqrt{3}}$$+\frac{1}{\sqrt{3}+\sqrt{4}}$+…+$\frac{1}{\sqrt{2013}+\sqrt{2014}}$+$\frac{1}{\sqrt{2014}+\sqrt{2015}}$
=$\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+$\sqrt{4}$-$\sqrt{3}$+…+$\sqrt{2014}$-$\sqrt{2013}$+$\sqrt{2015}$-$\sqrt{2014}$
=$\sqrt{2015}$-1.
点评 此题主要考查了分母有理化,正确发现式子中变化规律是解题关键.


 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案科目:初中数学 来源: 题型:解答题
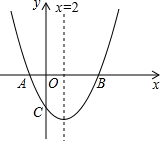 如图,经过点C(0,-4)的抛物线y=ax2+bx+c(a≠0)与x轴相交于A(-2,0),B两点.
如图,经过点C(0,-4)的抛物线y=ax2+bx+c(a≠0)与x轴相交于A(-2,0),B两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB为半圆O的直径,M为半圆内的一点,直线AM交半圆O于点C,直线BM交半圆O于点D,直线DC与直线AB交于点P,N为直径AB上的一点,且满足ON•OP=OB2,求证:MN⊥AB.
如图,AB为半圆O的直径,M为半圆内的一点,直线AM交半圆O于点C,直线BM交半圆O于点D,直线DC与直线AB交于点P,N为直径AB上的一点,且满足ON•OP=OB2,求证:MN⊥AB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 票价种类 | (A)夜场票 | (B)日通票 | (C)节假日通票 |
| 单价(元) | 80 | 120 | 150 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{3-\sqrt{5}}{2}$ | B. | $\frac{\sqrt{5}-1}{2}$ | C. | $\frac{1+\sqrt{5}}{2}$ | D. | $\frac{3-\sqrt{5}}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 34≤T≤37 | B. | 34≤T≤35 | C. | 33≤T≤35 | D. | 35≤T≤37 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 车型 | 甲 | 乙 | 丙 |
| 汽车运载量(吨/辆) | 5 | 8 | 10 |
| 汽车运费(元/辆) | 400 | 500 | 600 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com