
| ���� | �� | �� | �� |
| ��������������/���� | 5 | 8 | 10 |
| �����˷ѣ�Ԫ/���� | 400 | 500 | 600 |
���� ��1����������Ҫ���ֳ���x����һ�ֳ���y����������õ�����ϵ�����˷�8200Ԫ������������120�֣����ݵ�����ϵ�г������鼴�ɣ�
��2����׳���a�����ҳ���b����������У�14-a-b������������÷���5a+8b+10��14-a-b��=120���ټ���������⼴�ɣ�
��� �⣺��1������Ҫ���ֳ���x����һ�ֳ���y����������ã�
$\left\{\begin{array}{l}{5x+8y=120}\\{400x+500y=8200}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{x=8}\\{y=10}\end{array}\right.$��
����Ҫ���ֳ���8����һ�ֳ���10����
��2����׳���a�����ҳ���b����������У�14-a-b������������ã�
5a+8b+10��14-a-b��=120��
�����5a+2b=20��
��a=4-$\frac{2}{5}$b��
��a��b��14-a-b����������
��bֻ�ܵ���5���Ӷ�a=2��14-a-b=7��
��׳�2�����ҳ�5��������7����
�����˷�400��2+500��5+600��7=7500��Ԫ����
�𣺼׳�2�����ҳ�5��������7�������˷�7500Ԫ��
���� ���⿼��һԪһ�β���ʽ���Ӧ�ã�����ʵ�����е��¼�����ѧ˼����ϵ�������������г����̼�����⣮��������˼���δ֪����ʵ������ͨ��ɸѡ���ɵõ�δ֪���ľ���⣬���ַ���Ҫ���գ�


 ��У���˿��ֿ���ϵ�д�
��У���˿��ֿ���ϵ�д� �ƸԴ��ž�ϵ�д�
�ƸԴ��ž�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
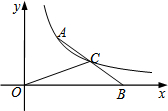 ��ͼ��AΪ˫����y=$\frac{4}{x}$��x��0����һ�㣬BΪx����������һ�㣬�߶�AB���е�Cǡ����˫�����ϣ����OBC�����Ϊ��������
��ͼ��AΪ˫����y=$\frac{4}{x}$��x��0����һ�㣬BΪx����������һ�㣬�߶�AB���е�Cǡ����˫�����ϣ����OBC�����Ϊ��������| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com