
【题目】直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系,曲线C1的极坐标方程为 ![]() ,直线l的参数方程为
,直线l的参数方程为  (t为参数),直线l与曲线C1交于A,B两点. (Ⅰ)求|AB|的长度;
(t为参数),直线l与曲线C1交于A,B两点. (Ⅰ)求|AB|的长度;
(Ⅱ)若曲线C2的参数方程为 ![]() (α为参数),P为曲线C2上的任意一点,求△PAB的面积的最小值.
(α为参数),P为曲线C2上的任意一点,求△PAB的面积的最小值.
【答案】解:(Ⅰ)∵ ![]() ,ρ2=2ρsinθ+2ρcosθ, ∴x2+y2=2x+2y,
,ρ2=2ρsinθ+2ρcosθ, ∴x2+y2=2x+2y,
即曲线C1的直角坐标系方程为(x﹣1)2+(y﹣1)2=2
直线l的直角坐标系方程为x+y﹣1=0
圆心C1到直线l的距离为d= ![]() =
= ![]() ,
,
∴ ![]()
(Ⅱ)曲线C2的直角坐标系方程为(x﹣3)2+(y﹣4)2=2
P到直l的最小距离为 ![]() ,
,
又 ![]() ,﹣1≤m≤3,
,﹣1≤m≤3,
∴△PAB的面积的最小值为 ![]()
【解析】(Ⅰ)利用两角和的正弦公式展开,即可求得曲线C1的直角坐标系方程,消去t,求得直线l的方程,利用点到直线的距离公式,即可求得|AB|的长度;(Ⅱ)同理求得曲线C2的直角坐标系方程,P到直l的最小距离为 ![]() ,求得
,求得 ![]() ,﹣1≤m≤3,即可求得△PAB的面积的最小值.
,﹣1≤m≤3,即可求得△PAB的面积的最小值.


科目:初中数学 来源: 题型:
【题目】如图反映的过程是:小强从家去菜地浇水,又去玉米地除草,然后回家.如果菜地和玉米地的距离为a千米,小强在玉米地除草比在菜地浇水多用的时间为b分钟,则a,b的值分别为( )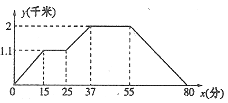
A.1.1,8
B.0.9,3
C.1.1,12
D.0.9,8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把函数f(x)= ![]() cos2x﹣sin2x的图象向右平移
cos2x﹣sin2x的图象向右平移 ![]() 个单位得到函数y=g(x)的图象,则函数y=g(x)在下列哪个区间是单调递减的( )
个单位得到函数y=g(x)的图象,则函数y=g(x)在下列哪个区间是单调递减的( )
A.[﹣ ![]() ,0]
,0]
B.[﹣π,0]
C.[﹣ ![]() ,
, ![]() ]
]
D.[0, ![]() ]
]
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网络营销部门为了统计某市网友2016年12月12日的网购情况,从该市当天参与网购的顾客中随机抽查了男女各30人,统计其网购金额,得到如下频率分布直方图:
网购达人 | 非网购达人 | 合计 | |
男性 | 30 | ||
女性 | 12 | 30 | |
合计 | 60 |
若网购金额超过2千元的顾客称为“网购达人”,网购金额不超过2千元的顾客称为“非网购达人”.
(Ⅰ)若抽取的“网购达人”中女性占12人,请根据条件完成上面的2×2列联表,并判断是否有99%的把握认为“网购达人”与性别有关?
(Ⅱ)该营销部门为了进一步了解这60名网友的购物体验,从“非网购达人”、“网购达人”中用分层抽样的方法确定12人,若需从这12人中随机选取3人进行问卷调查.设ξ为选取的3人中“网购达人”的人数,求ξ的分布列和数学期望.
(参考公式: ![]() ,其中n=a+b+c+d)
,其中n=a+b+c+d)
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若存在正实数m,使得关于x的方程x+a(2x+2m﹣4ex)[ln(x+m)﹣lnx]=0成立,其中e为自然对数的底数,则实数a的取值范围是( )
A.(﹣∞,0)
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知椭圆C: ![]() 的焦距为2,点Q(
的焦距为2,点Q( ![]() ,0)在直线l:x=3上.
,0)在直线l:x=3上.
(1)求椭圆C的标准方程;
(2)若O为坐标原点,P为直线l上一动点,过点P作直线与椭圆相切点于点A,求△POA面积S的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知曲线C1的参数方程为 ![]() (t为参数),以原点O为极点,以x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为
(t为参数),以原点O为极点,以x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为 ![]() . (I)求曲线C2的直角坐标系方程;
. (I)求曲线C2的直角坐标系方程;
(II)设M1是曲线C1上的点,M2是曲线C2上的点,求|M1M2|的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数f(x)=2cos(ωx﹣φ)(ω>0,φ∈[0,π]的部分图象如图所示,若A( ![]() ,
, ![]() ),B(
),B( ![]() ,
, ![]() ),则函数f(x)的单调增区间为( )
),则函数f(x)的单调增区间为( ) 
A.[﹣ ![]() +2kπ,
+2kπ, ![]() +2kπ](k∈Z)
+2kπ](k∈Z)
B.[ ![]() +2kπ,
+2kπ, ![]() +2kπ](k∈Z)
+2kπ](k∈Z)
C.[﹣ ![]() +kπ,
+kπ, ![]() +kπ](k∈Z)
+kπ](k∈Z)
D.[ ![]() +kπ,
+kπ, ![]() +kπ](k∈Z)
+kπ](k∈Z)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com