
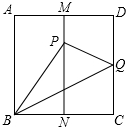
 如图,已知正方形纸片ABCD,M,N分别是AD、BC的中点,把BC边向上翻折,使点C恰好落在MN上的P点处,BQ为折痕,
如图,已知正方形纸片ABCD,M,N分别是AD、BC的中点,把BC边向上翻折,使点C恰好落在MN上的P点处,BQ为折痕,分析 (1)根据折叠的性质可知:BN=$\frac{1}{2}$BP,从而可知∠BPN的值,再根据∠PBQ=∠CBQ,可将∠PBQ的角度求出∠PBQ的度数;
(2)由特殊锐角三角函数求得PN=$\frac{\sqrt{3}}{2}$,然后可求得PM的长.
解答 解:(1)根据折叠的性质知:BP=BC,∠PBQ=∠CBQ,
∴BN=$\frac{1}{2}$BC=$\frac{1}{2}$BP,
∵∠BNP=90°,
∴∠BPN=30°,
∴∠PBQ=$\frac{1}{2}$×60°=30°.
(2)在Rt△PBN中,PN=PB•sin60°=1×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{2}$,
MP=NM-PN=1-$\frac{\sqrt{3}}{2}$=$\frac{2-\sqrt{3}}{2}$.
点评 本题主要考查的是翻折的性质,掌握翻折的性质是解题的关键.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com