
 已知等腰Rt△ABC与等腰Rt△DBE,F为AE中点,G为CD中点,连结GF.判断FG与DC的位置关系和数量关系.
已知等腰Rt△ABC与等腰Rt△DBE,F为AE中点,G为CD中点,连结GF.判断FG与DC的位置关系和数量关系. 分析 延长ED交AC的延长线于M,连接FC、FD、FM,由四边形BDMC是矩形,则BD=CM=DE.由于△DEB和△ABC都是等腰直角三角形,∠BED=∠A=45°,因此∠AEM=∠A=45°,得出△AEM是等腰直角三角形,F是斜边AE的中点,因此MF=EF,∠AMF=∠BED=45°,那么这两个角的补角也应当相等,由此可得出∠DEF=∠FMC,于是△DEF≌△CMF,可得到DF=FC,即△DFC是等腰三角形,根据△DEF≌△CMF,得出∠MFC=∠DFE,又∠MFC+∠CFE=90°,因此∠DFE+∠CFE=∠DFC=90°,得出△DFC是等腰直角三角形,所以FG⊥CD,FG=$\frac{1}{2}$CD.
解答 FG⊥CD,FG=$\frac{1}{2}$CD.
证明:延长ED交AC的延长线于M,连接FC、FD、FM,
∴四边形BCMD是矩形.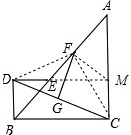
∴CM=BD.
又△ABC和△BDE都是等腰直角三角形
∴ED=BD=CM.
∵∠AEM=∠A=45°,
∴△AEM是等腰直角三角形.
又F是AE的中点,
∴MF⊥AE,EF=MF,∠EDF=∠MCF.
∵在△EFD和△MFC中
$\left\{\begin{array}{l}{DE=MC}\\{∠DEF=∠CMF}\\{EF=MF}\end{array}\right.$,
∴△EFD≌△MFC.
∴FD=FC,∠EFD=∠MFC.
又∠EFD+∠DFM=90°,
∴∠MFC+∠DFM=90°.
即△CDF是等腰直角三角形,
又G是CD的中点,
∴FG⊥CD,FG=$\frac{1}{2}$CD.
点评 本题主要考查了等腰直角三角形的判定与性质、全等三角形的判定与性质,构建全等三角形来证明线段和角相等是解题的关键.


科目:初中数学 来源: 题型:解答题
 没有量角器,利用刻度尺或三角板也能画出一个角的平分线吗?下面是小彬的做法,他的画法正确吗?请说明理由.
没有量角器,利用刻度尺或三角板也能画出一个角的平分线吗?下面是小彬的做法,他的画法正确吗?请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
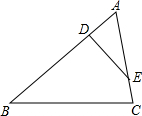 如图,D,E分别是△ABC的边AB,AC上的点,$\frac{BD}{AD}$=$\frac{AE}{CE}$=3,且∠AED=∠B,则△AED与△ABC的面积比是( )
如图,D,E分别是△ABC的边AB,AC上的点,$\frac{BD}{AD}$=$\frac{AE}{CE}$=3,且∠AED=∠B,则△AED与△ABC的面积比是( )| A. | 1:2 | B. | 1:3 | C. | 3:16 | D. | 4:9 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
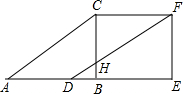 将Rt△ABC沿直角边AB向右平移2个单位得到Rt△DEF,如图,若AB=4,∠ABC=90°,且△ABC的面积为6个平方单位,求:
将Rt△ABC沿直角边AB向右平移2个单位得到Rt△DEF,如图,若AB=4,∠ABC=90°,且△ABC的面积为6个平方单位,求:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
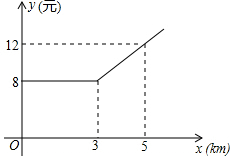 某市出租车计费方法如图所示,x(km)表示行驶里程,y(元)表示车费,若某乘客有一次乘出租车的车费为42元,则这位乘客乘车的里程为20km.
某市出租车计费方法如图所示,x(km)表示行驶里程,y(元)表示车费,若某乘客有一次乘出租车的车费为42元,则这位乘客乘车的里程为20km.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com