
分析 设第n个等式为an(n为正整数),分析给定的等式找出变化规律“an=(2n+1)2-(2n-1)2=8n”,依此规律即可得出结论.
解答 解:设第n个等式为an(n为正整数),
观察,发现规律:a1=32-12=(2×1+1)2-(2×1-1)2=8×1,a2=52-32=(2×2+1)2-(2×2-1)2=8×2,a3=72-52=(2×3+1)2-(2×3-1)2=8×3,a4=92-72=(2×4+1)2-(2×4-1)28×4,…,
∴an=(2n+1)2-(2n-1)2=8n.
当2n-1=103,即n=54时,
1052-1032=8×54=432.
点评 本题考查了规律型中的数字的变化类,根据数据的变化找出变化规律“an=(2n+1)2-(2n-1)2=8n”是解题的关键.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:解答题
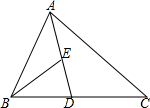 如图,AD是△ABC的中线,BE是△ABD的中线.
如图,AD是△ABC的中线,BE是△ABD的中线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,MN是⊙O的直径.
如图,MN是⊙O的直径.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
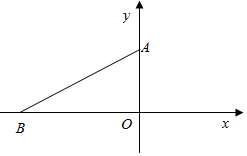 如图,已知Rt△OAB,∠OAB=60°,∠AOB=90°,O点与坐标系原点重合,若点P在x轴上,且△APB是等腰三角形,则点P的坐标可能有( )个.
如图,已知Rt△OAB,∠OAB=60°,∠AOB=90°,O点与坐标系原点重合,若点P在x轴上,且△APB是等腰三角形,则点P的坐标可能有( )个.| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com