

分析 (1)如图1,先证明△ACD≌△ABE,得∠ACD=∠ABC,根据三角形内角和与平角定义得出结论;
(2)如图2,图形中有四个等腰三角形:分别是①△ACF是等腰三角形,②△ADG是等腰直角三角形,③△DEF是等腰直角三角形;④△ECD是等腰三角形;根据已知角的度数依次计算各角的度数,根据两个角相等的三角形是等腰三角形得出结论.
解答 证明:(1)如图1,∵∠BAC=∠EAD,
∴∠BAC+∠CAE=∠EAD+∠CAE,
即∠BAE=∠CAD,
∵AB=AC,AD=AE,
∴△ACD≌△ABE,
∴∠ACD=∠ABC,
∵∠BAC+∠ABC+∠ACB=180°,
∠ECD+∠ACD+∠ACB=180°,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠BAC+2∠ACB=180°,
∠ECD+2∠ACB=180°,
∴∠BAC=∠ECD;
(2)如图2,
①∵∠BAC=∠EAD=30°,
∴∠ABC=∠ACB=∠AED=∠ADE=75°,
由(1)得:∠ACD=∠ABC=75°,
∠DCE=∠BAC=30°,
∵AD⊥AB,
∴∠BAD=90°,
∴∠CAE=30°,
∴∠AFC=180°-30°-75°=75°,
∴∠ACF=∠AFC,
∴△ACF是等腰三角形,
②∵∠BCG=∠DCE=30°,∠ABC=75°,
∴∠G=45°,
在Rt△AGD中,∠ADG=45°,
∴△ADG是等腰直角三角形,
③∠EDF=75°-45°=30°,
∴∠DEF=∠DFE=75°,
∴△DEF是等腰直角三角形;
④∵∠ECD=∠EDC=30°,
∴△ECD是等腰三角形.
点评 首先掌握等腰三角形的判定方法:有两个角相等的三角形是等腰三角形,本题借助于证明两三角形全等得出对应角相等,并结合三角形的内角和定理求角的度数,正确做出判断.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
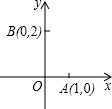 已知二次函数顶点在x轴上,且过A(1,0),B(0,2)两点.
已知二次函数顶点在x轴上,且过A(1,0),B(0,2)两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:在Rt△ABD中,∠ABD=90°,以直角边AB为直径作圆O交AD于C,取线段BD的中点E,连接CE交AB的延长线于P.
已知:在Rt△ABD中,∠ABD=90°,以直角边AB为直径作圆O交AD于C,取线段BD的中点E,连接CE交AB的延长线于P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,在△ABC中,AB=CB,∠ABC=90°,∠CAB=∠ACB,F为AB延长线上一点,点E在BC上,且∠EAB=∠FCB.
如图所示,在△ABC中,AB=CB,∠ABC=90°,∠CAB=∠ACB,F为AB延长线上一点,点E在BC上,且∠EAB=∠FCB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com