
【题目】(2011?常州)如图,DE是⊙O的直径,弦AB⊥CD,垂足为C,若AB=6,CE=1,则OC= ,CD= .
【答案】4;9
【解析】
连接OA构成直角三角形,先根据垂径定理,由DE垂直AB得到点C为AB的中点,由AB=6可求出AC的长,再设出圆的半径OA为x,表示出OC,根据勾股定理建立关于x的方程,求出方程的解即可得到x的值,即为圆的半径,通过观察图形可知,OC等于半径减1,CD等于半径加OC,把求出的半径代入即可得到答案.
解:连接OA,

∵直径DE⊥AB,且AB=6
∴AC=BC=3,
设圆O的半径OA的长为x,则OE=OD=x
∵CE=1,
∴OC=x-1,
在Rt△AOC中,根据勾股定理得:
x2-(x-1)2=32,化简得:x2-x2+2x-1=9,
即2x=10,
解得:x=5
所以OE=5,则OC=OE-CE=5-1=4,CD=OD+OC=9.
故答案为:4;9


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】高速铁路列车(简称:高铁)是人们出行的重要交通工具:已知高铁平均速度是普通铁路列车(简称:普客)平均速度的的3倍.同样行驶690km,高铁比普客少用4.6h.
(1)求高铁的平均速度.
(2)某天王老师乘坐8:40出发的高铁,到里程1050km的A市参加当天14:00召开的会议.若他从A市高铁站到会议地点最多还需要1.5h,试问在高铁准点到达的情况下,他能在开会之前赶到会议地点吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,学校环保社成员想测量斜坡CD旁一棵树AB的高度,他们先在点C处测得树顶B的仰角为60°,然后在坡顶D测得树顶B的仰角为30°,已知DE⊥EA,斜坡CD的长度为30m,DE的长为15m,则树AB的高度是_____m.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,△ABC中,∠ACB=90°,AC=BC,点E是BC上一点,连接AE.
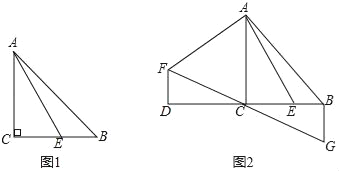
(1)如图1,当∠BAE=15°,CE=![]() 时,求AB的长.
时,求AB的长.
(2)如图2,延长BC至D,使DC=BC,将线段AE绕点A顺时针旋转90°得线段AF,连接DF,过点B作BG⊥BC,交FC的延长线于点G,求证:BG=BE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,反比例函数y=![]() (k≠0)的图象与一次函数y=ax+b(a≠0)的图象交于A、B两点,过点A作AH⊥y轴,垂足为H,若OH=4,sin∠AOH=
(k≠0)的图象与一次函数y=ax+b(a≠0)的图象交于A、B两点,过点A作AH⊥y轴,垂足为H,若OH=4,sin∠AOH=![]() ,点B的坐标(6,n).
,点B的坐标(6,n).
(1)求反比例函数和一次函数的解析式.
(2)求△AOB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,BD,CE分别是AC,AB边上的高,BD, CE交于O,则图中共有相似三角形( )

A. 5对 B. 6对 C. 7对 D. 8对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在△ABC中,AB=13,BC=12,点D,E分别是AB,BC的中点,连接DE,CD,如果DE=2.5,那么△ACD的周长是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校九年级男生的体能情况,体育老师随机抽取部分男生进行引体向上测试,并对成绩进行了统计,绘制出如下的统计图①和图②,请跟进相关信息,解答下列问题:
(Ⅰ)本次抽测的男生人数为 ,图①中m的值为 ;
(Ⅱ)求本次抽测的这组数据的平均数、众数和中位数;
(Ⅲ)若规定引体向上5次以上(含5次)为体能达标,根据样本数据,估计该校350名九年级男生中有多少人体能达标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=1,AD=![]() ,BD=2,∠ABC+∠ADC=180°,CD=
,BD=2,∠ABC+∠ADC=180°,CD=![]() .
.
(1)判断△ABD的形状,并说明理由;
(2)求BC的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com