
 张宇和孙宁两人同时从自己家出发到对方家去,张宇以每秒3米的速度走向张宇家,孙宁也以一定的速度走向张宇家.如图是两人出发后,时间与两人之间距离关系的图象.
张宇和孙宁两人同时从自己家出发到对方家去,张宇以每秒3米的速度走向张宇家,孙宁也以一定的速度走向张宇家.如图是两人出发后,时间与两人之间距离关系的图象.分析 (1)由图象可知,两人行走42秒时,两人相遇,根据路程=速度×时间,即可解答;
(2)设孙宁的速度是每秒x米,根据两人相遇,可路程方程42(3+x)=210,即可解答;
(3)点A表示张宇到达孙宁家所用的时间,点B表示孙宁到达张宇家所用的时间,根据时间=路程÷速度即可解答.
解答 解:(1)3×42=126(米),
答:两人在距离张宇家126米的地方相遇.
(2)设孙宁的速度是每秒x米,
根据题意可得:42(3+x)=210,
解得:x=2,
答:孙宁的速度是每秒2米.
(3)210÷3=70(秒),210÷2=105(秒),
∴图象中A、B表示的数为70、107.
点评 本题考查了一次函数的应用,读懂题目信息并准确识图理解函数图象的横坐标与纵坐标的实际意义以及行走过程是解题的关键.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (一)问题背景:小明是爱学习的人,通过网络搜索到有5种求三角形面积公式的方法.
(一)问题背景:小明是爱学习的人,通过网络搜索到有5种求三角形面积公式的方法.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
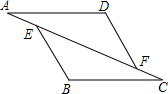 如图,已知:在△AFD和△CEB中,点A,E,F,C在同一条直线上,AE=CF,∠B=∠D,AD∥BC,请问:AD与BC相等吗?为什么?
如图,已知:在△AFD和△CEB中,点A,E,F,C在同一条直线上,AE=CF,∠B=∠D,AD∥BC,请问:AD与BC相等吗?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知点A(1,c)和点B(3,d)是直线y=k1x+b与双曲线y=$\frac{{k}_{2}}{x}$(k2>0)的交点
已知点A(1,c)和点B(3,d)是直线y=k1x+b与双曲线y=$\frac{{k}_{2}}{x}$(k2>0)的交点查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com