
����Ŀ��ij�������۽���Ϊ2Ԫ��ѩ�⣬�������з��֣�����Ʒ�������۵���x��Ԫ������������y������֮�������¹�ϵ��
�����۵���x��Ԫ�� | 3 | 4 | 5 | 6 |
��������y������ | 40 | 30 | 24 | 20 |
��1���²Ⲣȷ��y��x֮��ĺ�����ϵʽ��
��2�������Ʒ��������ΪW����W��x�ĺ�����ϵʽ������۾ֹ涨����Ʒ�����Ϊ10Ԫ/�������Ƿ��������Ʒ������������������������������˵�����ɣ�
���𰸡���1��![]() ����2��96Ԫ.
����2��96Ԫ.
�������������������1��Ҫȷ��y��x֮��ĺ�����ϵʽ��ͨ���۲�������ݣ����Է���x��y�ij˻�����ͬ�ģ�����120�����Կ�֪y��x�ɷ��������ô���ϵ������⼴�ɣ�
��2������Ҫ֪��������=�����۵���x-2��������������y�������Ϳ���ȷ��w��x�ĺ�����ϵʽ��Ȼ�������Ŀ���ۼ���߲�����10Ԫ/�����Ϳ����������������������ʱ�������۵���x��
����������⣺��1����3��40=120��4��30=120��5��24=120��6��20=120����y��x�ķ�������������![]() ��kΪ������k��0�����ѵ㣨3��40������ã�k=120������
��kΪ������k��0�����ѵ㣨3��40������ã�k=120������ ![]() ��
��
��2����W=��x��2��y=120��![]() ��
��
����x��10������x=10��W���=96��Ԫ����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
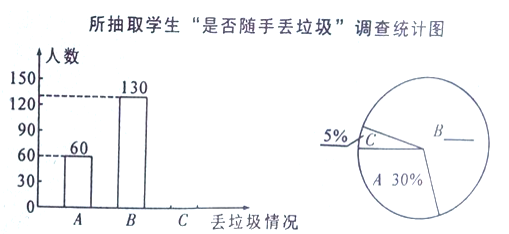
����Ŀ������������أ����ϸ���������ij��ѧΪ���˽����꼶ѧ�������һ�������ʵ�����ѧУ�������̴������꼶ѧ���������ȡ�˲���ѧ���������ѧ�����Ƿ����ֶ���������һ����������ʾ����飬����һ�����Ϊ��![]() �����Ӳ����ֶ�������
�����Ӳ����ֶ�������![]() ����ż�����ֶ�������
����ż�����ֶ�������![]() �����������ֶ��������Ҫ��ÿλ�������ѧ�����������������ѡһ����ֻ��ѡһ��ֽ����������Ƴ�����������������ͳ��ͼ���������������Ϣ������������⣺
�����������ֶ��������Ҫ��ÿλ�������ѧ�����������������ѡһ����ֻ��ѡһ��ֽ����������Ƴ�����������������ͳ��ͼ���������������Ϣ������������⣺
��1����ȫ����ͳ��ͼ������ͳ��ͼ��
��2��ͼ����ż�����ֶ��������������ε�Բ�Ľ�Ϊ______________��
��3������У���꼶����1500��ѧ����������Ƹ��꼶ѧ�������������ֶ���������ѧ��Լ�ж����ˣ�̸̸��Ŀ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʦ��ѧ������һ���⣺
��(2a+b)(2a��b)+2(2a��b)2+(2ab2��16a2b)��(��2a)��ֵ������a��![]() ��b����1��ͬѧ�ǿ�����Ŀ����ͬ�Ŀ�����С��˵������b����1�Ƕ���ģ���С��˵������������������Ͳ��������������Բ����࣮��
��b����1��ͬѧ�ǿ�����Ŀ����ͬ�Ŀ�����С��˵������b����1�Ƕ���ģ���С��˵������������������Ͳ��������������Բ����࣮��
(1)����Ϊ����˭˵���е�����Ϊʲô��
(2)��xm���ڱ��}����Ľ��������x2m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
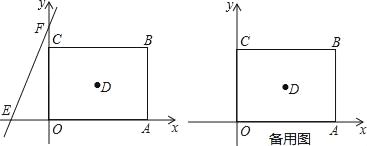
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������OABC�ı߳�Ϊa��ֱ��y��bx+c��x����E����y����F����a��b��c�ֱ����㩁��a��4��2��0��c��![]() +8.
+8.
��1����ֱ��y��bx+c�Ľ���ʽ��ֱ��д��������OABC�ĶԽ��ߵĽ���D�����ꣻ
��2��ֱ��y��bx+c��x����������ÿ���ƶ�1����λ���ȵ��ٶ�ƽ�ƣ���ƽ�Ƶ�ʱ��Ϊt�룬���Ƿ����t��ֵ��ʹֱ��EFƽ��������OABC������������ڣ������t��ֵ���������ڣ���˵�����ɣ�
��3����PΪ������OABC�ĶԽ���AC�ϵĶ��㣨�˵�A��C���⣩��PM��PO����ֱ��AB��M����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����4��5����ͼ�У�����ÿ��С�����α߳���Ϊ1������ABCD�������EFGHK�Ķ����ΪС�����εĶ��㣮
��1����BΪλ�����ģ�������ͼ�����ı���A��BC��D�䣬ʹ�ı���A��BC��D�������ABCDλ�ƣ���λ�Ʊ�Ϊ2��1��
��2����1�����ı���A��BC��D���������EFGHK�ص����ֵ��ܳ���������������ţ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��![]() �ֱ�
�ֱ�![]() �ᣬ
�ᣬ![]() ����A��B���㣬��CΪOB���е㣬��D�ڵڶ����ޣ����ı���AOCDΪ���Σ�
����A��B���㣬��CΪOB���е㣬��D�ڵڶ����ޣ����ı���AOCDΪ���Σ�

��1��ֱ��д����A��B�����꣬����ֱ��AB��CD����E�����ꣻ
��2������P�ӵ�C���������߶�CD��ÿ��1����λ���ȵ��ٶ����յ�D�˶���ͬʱ������N�ӵ�A���������߶�AO��ÿ��1����λ���ȵ��ٶ����յ�O�˶�������P��![]() ������ΪH������NP�����P���˶�ʱ��Ϊ
������ΪH������NP�����P���˶�ʱ��Ϊ![]() �룮
�룮
������NPH�����Ϊ1����![]() ��ֵ��
��ֵ��
����Q�ǵ�B���ڵ�A�ĶԳƵ㣬��![]() �Ƿ�����Сֵ������У������Ӧ�ĵ�P�����ꣻ���û�У���˵�����ɣ�
�Ƿ�����Сֵ������У������Ӧ�ĵ�P�����ꣻ���û�У���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ���Rt��ABC�У���BAC=90�㣬D��AC���е㣬CE��BD�ڵ�E����BA���ӳ����ڵ�F����BF=12�����FBC�����Ϊ( )

A. 40 B. 46 C. 48 D. 50
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��̽����
(1)��ͼ�٣��ڵ���ֱ��������ABC�У���ACB=90����CMƽ�֡�ACB��AB�ڵ�M����DΪ����CM��һ�㣬�Ե�CΪ��ת���Ľ��߶�CD��ʱ����ת90��õ��߶�CE������DE������CB�ڵ�F������BD��BE
��գ�
���߶�BD��BE��������ϵΪ______��
���߶�BC��DE��λ�ù�ϵΪ______��
�ƹ㣺
(2)��ͼ�ڣ��ڵ���������ABC�У����ǡ�ACB=a����CMƽ�֡�ACB��AB�ڵ�M����DΪ��ABC�ⲿ����CM��һ�㣬�Ե�CΪ��ת���Ľ��߶�CD��ʱ����ת���ȵõ��߶�CE������DE��BD��BE���ж�(1)�еĽ����Ƿ��������˵�����ɣ�
Ӧ�ã�
(3)��ͼ�ۣ��ڵȱ�������ABC�У�AB=4����BMƽ�֡�ABC��AC�ڵ�M����DΪ����BM��һ�㣬�Ե�BΪ��ת���Ľ��߶�BD��ʱ����ת60��õ��߶�BE������DE������BA�ڵ�F������AD��AE������A��D��MΪ��������������AEFȫ��ʱ����ֱ��д��DE��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����14�֣�С����ij��װ�̳����������飬�˽���̳�Ϊ�˼���ӪҵԱ�Ĺ��������ԣ�ʵ�С���������=��������+�Ƽ����𡱵ķ����������������Ϣ��
ӪҵԱA�������ۼ���200������������2400Ԫ��
ӪҵԱB�������ۼ���300������������2700Ԫ��
����ӪҵԱ���»�������Ϊ![]() Ԫ������ÿ����װ����
Ԫ������ÿ����װ����![]() Ԫ��
Ԫ��
��1����![]() ��
��![]() ��ֵ��
��ֵ��
��2����ijӪҵԱ���������벻����3100Ԫ����ô����������Ҫ����װ���ټ���
��3���̳�Ϊ�˶����۷�װ���Թ˿��Ƽ�һ�ֹ���ʽ����������3������2������1������350Ԫ����������1������2������3������370Ԫ��ij�˿��빺��ס��ҡ�����һ���������Ԫ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com