
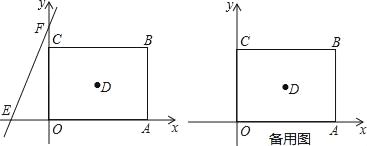
【题目】如图,在平面直角坐标系中,正方形OABC的边长为a.直线y=bx+c交x轴于E,交y轴于F,且a、b、c分别满足﹣(a﹣4)2≥0,c=![]() +8.
+8.
(1)求直线y=bx+c的解析式并直接写出正方形OABC的对角线的交点D的坐标;
(2)直线y=bx+c沿x轴正方向以每秒移动1个单位长度的速度平移,设平移的时间为t秒,问是否存在t的值,使直线EF平分正方形OABC的面积?若存在,请求出t的值;若不存在,请说明理由;
(3)点P为正方形OABC的对角线AC上的动点(端点A、C除外),PM⊥PO,交直线AB于M,求![]() 的值.
的值.
【答案】(1)y=2x+8,D(2,2);(2)存在,5;(3)![]() .
.
【解析】
试题(1)利用非负数的性质求出a,b,c的值,进而确定出直线y=bx+c,得到正方形的边长,即可确定出D坐标;
(2)存在,理由为:对于直线y=2x+8,令y=0求出x的值,确定出E坐标,根据题意得:当直线EF平移到过D点时正好平分正方形AOBC的面积,设平移后的直线方程为y=2x+t,将D坐标代入求出b的值,确定出平移后直线解析式,进而确定出此直线与x轴的交点,从而求出平移距离,得到t的值;
过P点作PQ∥OA,PH∥CO,交CO、AB于N、Q,交CB、OA于G、H,利用同角的余角相等得到一对角相等,再由一对直角相等,利用角平分线定理得到PH=PQ,利用AAS得到三角形OPH与三角形MPQ全等,得到OH=QM,根据四边形CNPG为正方形,得到PG=BQ=CN,由三角形CGP为等腰直角三角形得到CP=![]() GP=
GP=![]() BM,即可求出所求式子的值.
BM,即可求出所求式子的值.
试题解析:(1)∵-(a-4)2≥0,![]() ,
,
∴a=4,b=2,c=8,
∴直线y=bx+c的解析式为:y=2x+8,
∵正方形OABC的对角线的交点D,且正方形边长为4,
∴D(2,2);
(2)存在,理由为:
对于直线y=2x+8,
当y=0时,x=-4,
∴E点的坐标为(-4,0),
根据题意得:当直线EF平移到过D点时正好平分正方形AOBC的面积,
设平移后的直线为y=2x+t,
代入D点坐标(2,2),
得:2=4+t,即t=-2,
∴平移后的直线方程为y=2x-2,
令y=0,得到x=1,
∴此时直线和x轴的交点坐标为(1,0),平移的距离为1-(-4)=5,
则t=5秒;
(3)过P点作PQ∥OA,PH∥CO,交CO、AB于N、Q,交CB、OA于G、H,
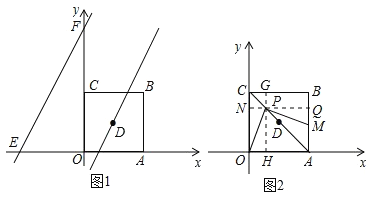
∵∠OPM=∠HPQ=90°,
∴∠OPH+∠HPM=90°,∠HPM+∠MPQ=90°,
∴∠OPH=∠MPQ,
∵AC为∠BAO平分线,且PH⊥OA,PQ⊥AB,
∴PH=PQ,
在△OPH和△MPQ中,
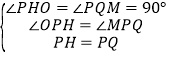 ,
,
∴△OPH≌△MPQ(AAS),
∴OH=QM,
∵四边形CNPG为正方形,
∴PG=BQ=CN,
∴CP=![]() PG=
PG=![]() BM,
BM,
即![]() .
.


科目:初中数学 来源: 题型:
【题目】口袋中装有四个大小完全相同的小球,把它们分别标号1,2,3,4,从中随机摸出一个球,记下数字后放回,再从中随机摸出一个球,利用树状图或者表格求出两次摸到的小球数和等于4的概率.
【答案】![]() .
.
【解析】试题分析:
根据题意列表如下,由表可以得到所有的等可能结果,再求出所有结果中,两次所摸到小球的数字之和为4的次数,即可计算得到所求概率.
试题解析:
列表如下:
1 | 2 | 3 | 4 | |
1 | (1,1) | (1,2) | (1,3) | (1,4) |
2 | (2,1) | (2,2) | (2,3) | (2,4) |
3 | (3,1) | (3,2) | (3,3) | (3,4) |
4 | (4,1) | (4,2) | (4,3) | (4,4) |
由表可知,共有16种等可能事件,其中两次摸到的小球数字之和等于4的有(3,1)、(2,2)和(1,3),共计3种,
∴P(两次摸到小球的数字之和等于4)=![]() .
.
【题型】解答题
【结束】
23
【题目】小亮同学想利用影长测量学校旗杆AB的高度,如图,他在某一时刻立1米长的标杆测得其影长为1.2米,同时旗杆的投影一部分在地面上BD处,另一部分在某一建筑的墙上CD处,分别测得其长度为9.6米和2米,求旗杆AB的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于第一象限C,D两点,坐标轴交于A、B两点,连结OC,OD(O是坐标原点).
的图象交于第一象限C,D两点,坐标轴交于A、B两点,连结OC,OD(O是坐标原点).
(1)利用图中条件,求反比例函数的解析式和m的值;
(2)求△DOC的面积.
(3)双曲线上是否存在一点P,使得△POC和△POD的面积相等?若存在,给出证明并求出点P的坐标;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王周末骑电动车从家里出发去商场买东西,当他骑了一段路时,想起要买一本书,于是原路返回到刚经过的新华书店,买到书后继续前往商场,如图是他离家的距离(米)与时间(分钟)之间的关系示意图,请根据图中提供的信息回答下列问题:
(1)在此变化过程中,自变量是 ,因变量是 .
(2)小王在新华书店停留了多长时间?
(3)买到书后,小王从新华书店到商场的骑车速度是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王老师家买了一套新房,其结构如图所示(单位:m).他打算将卧室铺上木地板,其余部分铺上地砖.
(1)木地板和地砖分别需要多少平方米?
(2)如果地砖的价格为每平方米x元,木地板的价格为每平方米3x元,那么王老师需要花多少钱?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一纸板的形状为正方形ABCD如图所示.其边长为10厘米,AD、BC与投影面β平行,AB、CD与投影面不平行,正方形在投影面β上的正投影为A1B1C1D1.若∠ABB1=45°,求投影面A1B1C1D1的面积.
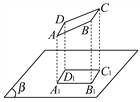
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售进价为2元的雪糕,在销售中发现,此商品的日销售单价x(元)与日销售量y(根)之间有如下关系:
日销售单价x(元) | 3 | 4 | 5 | 6 |
日销售量y(根) | 40 | 30 | 24 | 20 |
(1)猜测并确定y和x之间的函数关系式;
(2)设此商品销售利润为W,求W与x的函数关系式,若物价局规定此商品最高限价为10元/根,你是否能求出商品日销售最大利润?若能请求出,不能请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
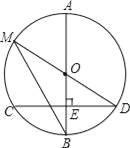
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E,且CD=24,点M在⊙O上,MD经过圆心O,联结MB.
(1)若BE=8,求⊙O的半径;
(2)若∠DMB=∠D,求线段OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某电器商场根据民众健康需要,代理销售某种家用空气净化器,其进价是200元/台.经过市场销售后发现:在一个月内,当售价是400元/台时,可售出200台,且售价每降低10元,就可多售出50台.若供货商规定这种空气净化器售价不能低于300元/台,代理销售商每月要完成不低于450台的销售任务.
(1)试确定月销售量y(台)与售价x(元/台)之间的函数关系式;
(2)求出售价x的范围;
(3)商场每月销售这种空气净化器所获得的利润为w(元),写出w关于x的关系?当售价x(元/台)定为多少时利润最大,最大是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com