
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于第一象限C,D两点,坐标轴交于A、B两点,连结OC,OD(O是坐标原点).
的图象交于第一象限C,D两点,坐标轴交于A、B两点,连结OC,OD(O是坐标原点).
(1)利用图中条件,求反比例函数的解析式和m的值;
(2)求△DOC的面积.
(3)双曲线上是否存在一点P,使得△POC和△POD的面积相等?若存在,给出证明并求出点P的坐标;若不存在,说明理由.

【答案】(1)、y=![]() ;m=1;(2)、7.5;(3)、(2,2)或(-2,-2).
;m=1;(2)、7.5;(3)、(2,2)或(-2,-2).
【解析】
试题分析:(1)、根据点C的坐标求出反比例函数解析式,根据反比例函数解析式求出m的值;(2)、首先求出一次函数的解析式,然后得出点A和点B的坐标,然后利用△OAB的面积-△BOC的面积-△AOD的面积求出△DOC的面积;(3)、根据对称性得出点P的坐标.
试题解析:(1)、将C(1,4)代入反比例函数解析式可得:k=4,则反比例函数解析式为:![]() ,
,
将D(4,m)代入反比例函数解析式可得:m=1;
(2)、根据点C和点D的坐标得出一次函数的解析式为:y=-x+5
则点A的坐标为(0,5),点B的坐标为(5,0)
∴S△DOC=5×5÷2-5×1÷2-5×1÷2=7.5
(3)、存在,利用点CD关于直线y=x对称,P(2,2)或P(-2,-2)


科目:初中数学 来源: 题型:
【题目】下列各小题中,都有OE平分∠AOC,OF平分∠BOC.
(1)如图①,若点A、O、B在一条直线上,∠EOF= ;
(2)如图②,若点A、O、B不在一条直线上,∠AOB=140°,则∠EOF= ;
(3)由以上两个问题发现:当∠AOC在∠BOC的外部时,∠EOF与∠AOB的数量关系是∠EOF= ;
(4)如图③,若OA在∠BOC的内部,∠AOB和∠EOF还存在上述的数量关系吗;请简单说明理由;



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个不透明口袋,装有分别标有数字1,2,3,4的4个小球(小球除数字不同外,其余都相同),另有3张背面完全一样、正面分别写有数字1,2,3的卡片.小敏从口袋中任意摸出一个小球,小颖从这3张背面朝上的卡片中任意摸出一张,然后计算小球和卡片上的两个数的积.
(1)请你用列表或画树状图的方法,求摸出的这两个数的积为6的概率;
(2)小敏和小颖做游戏,她们约定:若这两个数的积为奇数,小敏赢;否则,小颖赢.你认为该游戏公平吗?为什么?如果不公平,请你修改游戏规则,使游戏公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,,垂足分别为E,F.(1)、求证:△BED≌△CFD;(2)、若∠A=90°,求证:四边形DFAE是正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的有( ) ①不相交的两条直线是平行线;②在同一平面内,两条直线的位置关系有两种;
③若线段AB与CD没有交点,则AB∥CD;④若a∥b,b∥c,则a与c不相交.
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
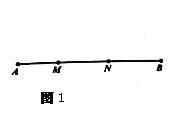
【题目】(本题满分10分)定义:如图1,点M,N把线段AB分割成AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点.
(1)已知点M,N是线段AB的勾股分割点,若AM=3,MN=5,求BN的长;
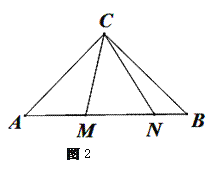
(2)如图2,在Rt△ABC中,AC=BC,点M,N在斜边AB上,![]() MCN=45,求证:点M,N是线段AB的勾股分割点.
MCN=45,求证:点M,N是线段AB的勾股分割点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c图象上部分点的坐标满足表格:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | … |
y | … | ﹣3 | ﹣2 | ﹣3 | ﹣6 | ﹣11 | … |
则该函数图象的顶点坐标为( )
A.(﹣3,﹣3)
B.(﹣2,﹣2)
C.(﹣1,﹣3)
D.(0,﹣6)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com