
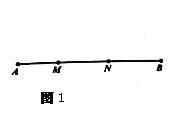
【题目】(本题满分10分)定义:如图1,点M,N把线段AB分割成AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点.
(1)已知点M,N是线段AB的勾股分割点,若AM=3,MN=5,求BN的长;
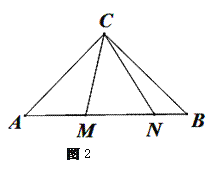
(2)如图2,在Rt△ABC中,AC=BC,点M,N在斜边AB上,![]() MCN=45,求证:点M,N是线段AB的勾股分割点.
MCN=45,求证:点M,N是线段AB的勾股分割点.
【答案】(1)当MN最长时,BN=4;
当BN最长时,BN=![]() ;…………4分
;…………4分
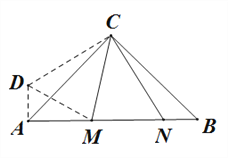 如图,过点A作AD⊥AB,且AD=BN
如图,过点A作AD⊥AB,且AD=BN
证 △ADC≌△BNC,∴CD=CN,∠ACD=∠BCN,
再证:∠MCD=∠BCM,
证 △MDC≌△MNC,∴MD=MN
在Rt△MDA中,![]()
∴![]()
∴点M,N是线段AB的勾股分割点.…………10分
【解析】试题分析:(1)分两种切线利用勾股定理即可解决问题;
(2)如图,过点A作AD⊥AB,且AD=BN.只要证明△ADC≌△BNC,推出CD=CN,∠ACD=∠BCN,再证明△MDC≌△MNC,可得MD=MN,由此即可解决问题.
试题解析:(1)当MN最长时,BN=![]() =4;
=4;
当BN最长时,BN=![]() =
=![]() ;
;
(2)如图,过点A作AD⊥AB,且AD=BN,
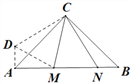
∵AD=BN,∠DAC=∠B=45°,AC=BC,
∴△ADC≌△BNC,
∴CD=CN,∠ACD=∠BCN,
∵∠MCN=45°,
∴∠DCA+∠ACM=∠ACM+∠BCN=45°,
∴∠MCD=∠BCM,
∴△MDC≌△MNC,
∴MD=MN,
在Rt△MDA中,AD2+AM2=DM2,
∴BN2+AM2=MN2,
∴点M,N是线段AB的勾股分割点。


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AD平分∠CAB.
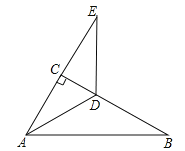
(1)求∠CAD的度数;
(2)延长AC至E,使CE=AC,求证:DA=DE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于第一象限C,D两点,坐标轴交于A、B两点,连结OC,OD(O是坐标原点).
的图象交于第一象限C,D两点,坐标轴交于A、B两点,连结OC,OD(O是坐标原点).
(1)利用图中条件,求反比例函数的解析式和m的值;
(2)求△DOC的面积.
(3)双曲线上是否存在一点P,使得△POC和△POD的面积相等?若存在,给出证明并求出点P的坐标;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像交于M(2,m)、N(-1-4) 两点.
的图像交于M(2,m)、N(-1-4) 两点.
(1)求反比例函数和一次函数的解析式;
(2)根据图像写出使反比例函数值大于一次函数值的x取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车匀速通过某段公路,所需时间t(h)与行驶速度v(km/h)满足函数关系:
t=![]() ,其图象为如图所示的一段曲线且端点为A(40,1)和B(m,0.5).
,其图象为如图所示的一段曲线且端点为A(40,1)和B(m,0.5).
(1)求k和m的值;(2)若行驶速度不得超过60 km/h,则汽车通过该路段最少需要多少时间?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,错误的是( )
A. 有两个内角分别是70°和40°的三角形是等腰三角形
B. 有两个内角相等的三角形是等边三角形
C. 一个外角平分线平行于一边的三角形是等腰三角形
D. 等边三角形一定是等腰三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
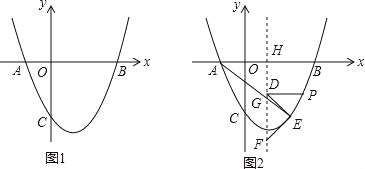
【题目】在平面直角坐标中,抛物线y=ax2﹣3ax﹣10a(a>0)分别交x轴于点A、B(点A在点B左侧),交y轴于点C,且OB=OC.
(1)求a的值;
(2)如图1,点P位抛物线上一动点,设点P的横坐标为t(t>0),连接AC、PA、PC,△PAC的面积为S,求S与t之间的函数关系式;
(3)如图2,在(2)的条件下,设对称轴l交x轴于点H,过P点作PD⊥l,垂足为D,在抛物线、对称轴上分别取点E、F,连接DE、EF,使PD=DE=EF,连接AE交对称轴于点G,直线y=kx﹣![]() k(k≠0)恰好经过点G,将直线y=kx﹣
k(k≠0)恰好经过点G,将直线y=kx﹣![]() k沿过点H的直线折叠得到对称直线m,直线m恰好经过点A,直线m与第四象限的抛物线交于另一点Q,若
k沿过点H的直线折叠得到对称直线m,直线m恰好经过点A,直线m与第四象限的抛物线交于另一点Q,若![]() =
=![]() ,求点Q的坐标.
,求点Q的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com