
【题目】在平面直角坐标中,抛物线y=ax2﹣3ax﹣10a(a>0)分别交x轴于点A、B(点A在点B左侧),交y轴于点C,且OB=OC.
(1)求a的值;
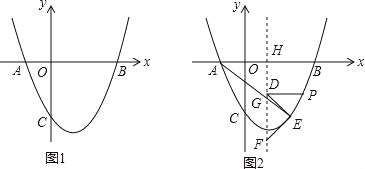
(2)如图1,点P位抛物线上一动点,设点P的横坐标为t(t>0),连接AC、PA、PC,△PAC的面积为S,求S与t之间的函数关系式;
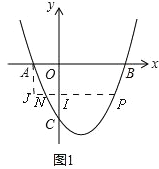
(3)如图2,在(2)的条件下,设对称轴l交x轴于点H,过P点作PD⊥l,垂足为D,在抛物线、对称轴上分别取点E、F,连接DE、EF,使PD=DE=EF,连接AE交对称轴于点G,直线y=kx﹣![]() k(k≠0)恰好经过点G,将直线y=kx﹣
k(k≠0)恰好经过点G,将直线y=kx﹣![]() k沿过点H的直线折叠得到对称直线m,直线m恰好经过点A,直线m与第四象限的抛物线交于另一点Q,若
k沿过点H的直线折叠得到对称直线m,直线m恰好经过点A,直线m与第四象限的抛物线交于另一点Q,若![]() =
=![]() ,求点Q的坐标.
,求点Q的坐标.
【答案】(1)a=![]() ;(2)S=
;(2)S= ![]() t2+t;(3)Q(
t2+t;(3)Q(![]() ,﹣
,﹣![]() ).
).
【解析】
试题分析:(1)令y=0,求出x轴交点坐标,再用OB=OC求出C点坐标,代入抛物线方程即可;(2)先求出直线AC解析式,再用t表示出PN代入面积公式计算即可;(3)依次求出直线AE的解析式为y=﹣x﹣2,直线WG的解析式为y=3x﹣8,直线KH的解析式为y=﹣2x+3,直线AV的解析式为y=﹣![]() x﹣
x﹣![]() ,即可.
,即可.
试题解析:(1)令y=0,则ax2﹣3ax﹣10a=0,
即a(x+2)(x﹣5)=0,
∴x1=﹣2,x2=5,
∴A(﹣2,0),B(5,0),
∴OB=5,
∵OB=OC,
∴OC=5,
∴C(0,﹣5),
∴﹣5=﹣10a,
∴a=![]() ;
;
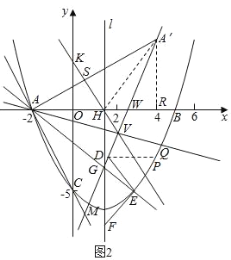
(2)如图1,
由(1)可知知抛物线解析式为y=![]() x2﹣
x2﹣![]() x﹣5,
x﹣5,
设直线AC的解析式为:y=k1x+b,把A、C两点坐标代入得:
 ,解得:
,解得: ,
,
∴y=﹣![]() x﹣5,
x﹣5,
∵点P的横坐标为t,则P(t,![]() t2﹣
t2﹣![]() t﹣5),
t﹣5),
过点P作PN∥x轴交AC于点N,
把y=![]() x2﹣
x2﹣![]() x﹣5,代入直线AC解析式y=﹣
x﹣5,代入直线AC解析式y=﹣![]() x﹣5中,
x﹣5中,
解得xN=﹣![]() t2+
t2+![]() t,
t,
∴N(﹣![]() t2+
t2+![]() t,
t,![]() t2﹣
t2﹣![]() t﹣5),
t﹣5),
∴PN=t﹣(﹣![]() t2+
t2+![]() t)=
t)=![]() t2+
t2+![]() t,
t,
S=S△ANP+S△CNP=![]() PN×AJ+
PN×AJ+![]() PN×AI
PN×AI
=![]() PN×OI+
PN×OI+![]() PN×CI
PN×CI
=![]() PN(OI+CI)
PN(OI+CI)
=![]() PN×OC
PN×OC
=![]() t2+t,
t2+t,
(3)由y=![]() x2﹣
x2﹣![]() x﹣5=
x﹣5=![]() (x﹣
(x﹣![]() )2﹣
)2﹣![]() ,
,
得抛物线的对称轴为直线x=![]() ,顶点坐标为(
,顶点坐标为(![]() ,﹣
,﹣![]() ),
),
∵![]() ,
,
∴设DP=5n,DF=8n,
∵DE=EP=5n,过点E作EM⊥l于点M,则DM=FM=![]() DF=4n,
DF=4n,
∴在Rt△DME中,EM=3n,
∴点P的横坐标为5n+![]() ,点E横坐标为3n+
,点E横坐标为3n+![]() ,
,
∴yP=![]() (5n+
(5n+![]() ﹣
﹣![]() )2﹣
)2﹣![]() =
=![]() n2﹣
n2﹣![]() ,
,
yE=![]() (3n+
(3n+![]() ﹣
﹣![]() )2﹣
)2﹣![]() =
=![]() n2﹣
n2﹣![]()
∴D(![]() ,
,![]() n2﹣
n2﹣![]() ),M(
),M(![]() ,
, ![]() n2﹣
n2﹣![]() ),
),
∴DM=![]() n2﹣
n2﹣![]() ﹣(
﹣(![]() n2﹣
n2﹣![]() )=8n2,
)=8n2,
∴8n2=4n,
∴n=![]() ,
,
∴E(3,﹣5),
∵A(﹣2,0),E(3,﹣5),
∴直线AE的解析式为y=﹣x﹣2,
令x=![]() ,则y=﹣x﹣2=﹣
,则y=﹣x﹣2=﹣![]() ﹣2=﹣
﹣2=﹣![]() ,
,
∴G(![]() ,﹣
,﹣![]() ),
),
∵直线y=kx﹣![]() k(k≠0)恰好经过点G,
k(k≠0)恰好经过点G,
∴﹣![]() =
=![]() k﹣
k﹣![]() k,
k,
∴k=3,
∴直线WG的解析式为y=3x﹣8,
如图2,
点A关于HK的对称点A′(m,3m﹣8),
∵A(﹣2,0),H(![]() ,0),
,0),
∴AH=![]() ,
,
∵HS垂直平分AA′,
∴A′H=AH=![]() ,
,
过A′作A′R⊥x轴于R,
在Rt△A′HR中,A′R2+HR2=A′H2,
∴(3m﹣8)2+(m﹣![]() )2=
)2=![]() ,
,
∴m1=![]() (舍),m2=
(舍),m2=![]() ,
,
∴A′(![]() ,
,![]() ),
),
∴tan∠A′AR=![]() ,
,
∵∠HAS+∠AHS=∠OKH+∠AHS=90°,
∴tan∠OKH=tan∠A′AR=![]() ,
,
∴tan∠OKH=![]() ,
,
∴OK=3,
∴K(0,3),
∴直线KH的解析式为y=﹣2x+3,
∵![]() ,
,
∴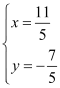 ,
,
∴V(![]() ,﹣
,﹣![]() ),
),
∵A(﹣2,0),
∴直线AV的解析式为y=﹣![]() x﹣
x﹣![]() ,
,
设Q(s, ![]() s2﹣
s2﹣![]() s﹣5),代入y=﹣
s﹣5),代入y=﹣![]() x﹣
x﹣![]() 中,
中,
![]() s2﹣
s2﹣![]() s﹣5=﹣
s﹣5=﹣![]() s﹣
s﹣![]() ,
,
∴s1=﹣2(舍),s2=![]() ,
,
∴Q(![]() ,﹣
,﹣![]() ).
).


科目:初中数学 来源: 题型:
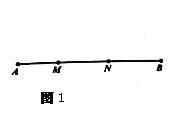
【题目】(本题满分10分)定义:如图1,点M,N把线段AB分割成AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点.
(1)已知点M,N是线段AB的勾股分割点,若AM=3,MN=5,求BN的长;
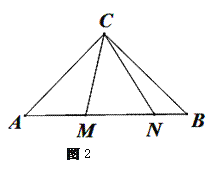
(2)如图2,在Rt△ABC中,AC=BC,点M,N在斜边AB上,![]() MCN=45,求证:点M,N是线段AB的勾股分割点.
MCN=45,求证:点M,N是线段AB的勾股分割点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c图象上部分点的坐标满足表格:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | … |
y | … | ﹣3 | ﹣2 | ﹣3 | ﹣6 | ﹣11 | … |
则该函数图象的顶点坐标为( )
A.(﹣3,﹣3)
B.(﹣2,﹣2)
C.(﹣1,﹣3)
D.(0,﹣6)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各组中的四条线段成比例的是( )
A.a=1,b=3,c=2,d=4
B.a=4,b=6,c=5,d=10
C.a=2,b=4,c=3,d=6
D.a=2,b=3,c=4,d=1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算下列各题.
(1)﹣1.3+(﹣1.7)﹣(﹣13)
(2)﹣30×( ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() )
)
(3)(﹣2)2×3+2×(﹣32)
(4)﹣2×( ![]() ﹣
﹣ ![]() )+|﹣7|.
)+|﹣7|.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AD平分∠BAC,O是AC的中点,连接DO,过点C作CE∥DA,交DO的延长线于点E,连接AE.

(1)求证:四边形ADCE是矩形;
(2)若F是CE上的动点(点F不与C、E重合),连接AF、DF、BE,请直接写出图2中与四边形ABDF面积相等的所有的三角形和四边形(四边形ABDF除外)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义一种对正整数n的“F运算”: (1.)当n为奇数时,结果为3n+5;
(2.)当n为偶数时,结果为 ![]() (其中k是使
(其中k是使 ![]() 为奇数的正整数),并且运算重复进行,
为奇数的正整数),并且运算重复进行,
例如,取n=26,则:![]()
若n=449,则第2014次“F运算”的结果是
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要从甲、乙两名运动员中选出一名参加“2016里约奥运会”100m比赛,对这两名运动员进行了10次测试,经过数据分析,甲、乙两名运动员的平均成绩均为10.05(s),甲的方差为0.024(s2),乙的方差为0.008(s2),则这10次测试成绩比较稳定的是 运动员.(填“甲”或“乙”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列关于变量x,y的关系式中:①3x-2y=5;②y=|x|;③2x-y2=10.其中y是x的函数的是( )
A. ①②③ B. ①② C. ①③ D. ②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com