
【题目】如图,在△ABC中,AB=AC,AD平分∠BAC,O是AC的中点,连接DO,过点C作CE∥DA,交DO的延长线于点E,连接AE.

(1)求证:四边形ADCE是矩形;
(2)若F是CE上的动点(点F不与C、E重合),连接AF、DF、BE,请直接写出图2中与四边形ABDF面积相等的所有的三角形和四边形(四边形ABDF除外)
【答案】(1)详见解析;(2)S四边形ABDF=S四边形ABDE.
【解析】
试题分析:(1)根据全等三角形的判定求出△ADO≌△CEO,求出OD=OE,根据平行四边形的判定得出四边形ADCE是平行四边形,再根据矩形的判定得出即可;(2)根据面积公式和等底等高的三角形的面积相等得出即可.
试题解析:(1)证明:∵CE∥DA,
∴∠OCE=∠OAD,
∵O为AC的中点,
∴OA=OC,
在△ADO和△CEO中
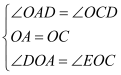
∴△ADO≌△CEO(ASA),
∴OD=OE,
∵OA=OC,
∴四边形ADCE是平行四边形,
∵AB=AC,AD平分∠BAC,
∴AD⊥BC,
∴∠ADC=90°,
∴平行四边形ADCE是矩形;
(2)解:图2中与四边形ABDF面积相等的所有的三角形和四边形有△ABC,△BCE,矩形ADCE,四边形ABDE,
理由是:∵△ACD和△AFD的面积相等(等底等高的三角形面积相等),
∴S△ADC=S△ADF,
∴S△ADC+S△ADB=S△ADF+S△ADB,
∴S四边形ABDF=S△ABC;
∵S△BCE=S△ABC,
∴S四边形ABDF=S△BCE;
∵S△ADB=S△ADC,S△ADF=S△AEC,
∴S四边形ABDF=S矩形ADCE;
∵S△ADF=S△ADE,
∴都加上△ADB的面积得:S四边形ABDF=S四边形ABDE.


科目:初中数学 来源: 题型:
【题目】如图,这是由8个同样大小的立方体组成的魔方,体积为8cm3 . 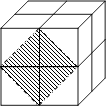
(1)求出这个魔方的棱长.
(2)图中阴影部分是一个正方形,求出阴影部分的面积及其边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
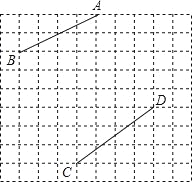
【题目】如图,在每个小正方形的边长均为1的方格纸中,有线段AB和线段CD,点A、B、C、D均在小正方形的顶点上.
(1)在方格纸中画以AB为斜边的等腰直角三角形ABE;
(2)在方格纸中画以CD为一边的三角形CDF,点F在小正方形的顶点上,且三角形CDF的面积为5,tan∠DCF=![]() ,连接EF,并直接写出线段EF的长.
,连接EF,并直接写出线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
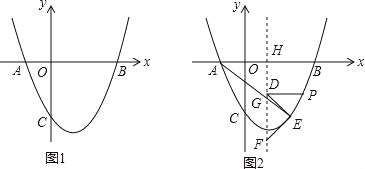
【题目】在平面直角坐标中,抛物线y=ax2﹣3ax﹣10a(a>0)分别交x轴于点A、B(点A在点B左侧),交y轴于点C,且OB=OC.
(1)求a的值;
(2)如图1,点P位抛物线上一动点,设点P的横坐标为t(t>0),连接AC、PA、PC,△PAC的面积为S,求S与t之间的函数关系式;
(3)如图2,在(2)的条件下,设对称轴l交x轴于点H,过P点作PD⊥l,垂足为D,在抛物线、对称轴上分别取点E、F,连接DE、EF,使PD=DE=EF,连接AE交对称轴于点G,直线y=kx﹣![]() k(k≠0)恰好经过点G,将直线y=kx﹣
k(k≠0)恰好经过点G,将直线y=kx﹣![]() k沿过点H的直线折叠得到对称直线m,直线m恰好经过点A,直线m与第四象限的抛物线交于另一点Q,若
k沿过点H的直线折叠得到对称直线m,直线m恰好经过点A,直线m与第四象限的抛物线交于另一点Q,若![]() =
=![]() ,求点Q的坐标.
,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
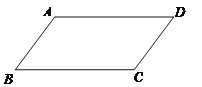
【题目】如图,已知AD∥BC,要使四边形ABCD为平行四边形,需要增加的一个条是:_____.(只填一个你认为正确的条件即可,不添加任何线段与字母)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com