
【题目】下列各小题中,都有OE平分∠AOC,OF平分∠BOC.
(1)如图①,若点A、O、B在一条直线上,∠EOF= ;
(2)如图②,若点A、O、B不在一条直线上,∠AOB=140°,则∠EOF= ;
(3)由以上两个问题发现:当∠AOC在∠BOC的外部时,∠EOF与∠AOB的数量关系是∠EOF= ;
(4)如图③,若OA在∠BOC的内部,∠AOB和∠EOF还存在上述的数量关系吗;请简单说明理由;



【答案】(1)90°;(2)70°;(3)![]() ∠AOB;(4)存在.
∠AOB;(4)存在.
【解析】试题分析:
(1)由已知条件可得∠EOF=∠EOC+∠FOC=![]() ∠AOC+
∠AOC+![]() ∠BOC=
∠BOC=![]() ∠AOB=90°;
∠AOB=90°;
(2)由已知条件可得∠EOF=∠EOC+∠FOC=![]() ∠AOC+
∠AOC+![]() ∠BOC=
∠BOC=![]() ∠AOB=70°;
∠AOB=70°;
(3)由(1)和(2)可知,当∠AOC在∠BOC的外部时,∠EOF与∠AOB的数量关系是∠EOF=![]() ∠AOB;
∠AOB;
(4)存在,由OE平分∠AOC,OF平分∠BOC可得∠EOC=![]() ∠AOC,∠FOC=
∠AOC,∠FOC=![]() ∠BOC,结合∠BOC=∠AOC+∠AOB可得∠FOC=
∠BOC,结合∠BOC=∠AOC+∠AOB可得∠FOC=![]() ∠AOC+
∠AOC+![]() ∠AOB,再由∠EOF=∠FOC-∠EOC计算可得结论.
∠AOB,再由∠EOF=∠FOC-∠EOC计算可得结论.
试题解析:
(1)∵OE平分∠AOC,OF平分∠BOC,
∴∠EOC=![]() ∠AOC,∠FOC=
∠AOC,∠FOC=![]() ∠BOC,
∠BOC,
又∵∠EOF=∠EOC+∠FOC,
∴∠EOF=![]() ∠AOC+
∠AOC+![]() ∠BOC=
∠BOC=![]() (∠AOC+∠BOC)=
(∠AOC+∠BOC)= ![]() ∠AOB,
∠AOB,
∵点A、O、B在一条直线上,
∴∠AOB=180°,
∴∠EOF=90°.
(2)∵OE平分∠AOC,OF平分∠BOC,
∴∠EOC=![]() ∠AOC,∠FOC=
∠AOC,∠FOC=![]() ∠BOC,
∠BOC,
又∵∠EOF=∠EOC+∠FOC,
∴∠EOF=![]() ∠AOC+
∠AOC+![]() ∠BOC=
∠BOC=![]() (∠AOC+∠BOC)=
(∠AOC+∠BOC)= ![]() ∠AOB,
∠AOB,
∵∠AOB=140°,
∴∠EOF=70°.
(3)由(1)、(2)可知,∠EOF=![]() ∠AOB;
∠AOB;
(4)存在,理由如下:
∵OE平分∠AOC,OF平分∠BOC,
∴∠EOC=![]() ∠AOC,∠FOC=
∠AOC,∠FOC=![]() ∠BOC.
∠BOC.
又∵∠EOF=∠FOC-∠EOC,
∴∠EOF=∠FOC-∠EOC=![]() (∠BOC-∠AOC),
(∠BOC-∠AOC),
又∵∠BOC-∠AOC=∠AOB,
∴∠EOF=![]() ∠AOB.
∠AOB.


科目:初中数学 来源: 题型:
【题目】阅读材料:设一元二次方程![]() (
(![]() ≠0)的两根为
≠0)的两根为![]() ,
,![]() ,则两根与方程的系数之间有如下关系:
,则两根与方程的系数之间有如下关系:![]() +
+![]() =-
=-![]() ,
,![]() ·
·![]() =
=![]() .根据该材料完成下列填空:
.根据该材料完成下列填空:
已知m,n是方程x2-2014x+2015=0的两根,则:
(1)m+n=_____,mn=_____;
(2)(m2-2015m+2016)(n2-2015n+2016)=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC
(2)若AB=4,AD=3![]() ,AE=3,求AF的长.
,AE=3,求AF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AD平分∠CAB.
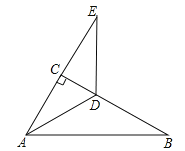
(1)求∠CAD的度数;
(2)延长AC至E,使CE=AC,求证:DA=DE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,边AB、AC的垂直平分线分别交BC于D、E.
(1)若BC=10,则△ADE周长是多少?为什么?
(2)若∠BAC=128°,则∠DAE的度数是多少?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
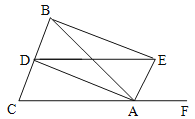
【题目】如图,△ABC中,AB=AC,AD、AE分别是∠BAC和∠BAC和外角的平分线,BE⊥AE.
(1)求证:DA⊥AE;
(2)试判断AB与DE是否相等?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式从左到右的变形属于因式分解的是( )
A. (m-2)(m-3)=(3-m)(2-m) B. a2-2a+3=(a-1)2+2
C. (x+1)(x-1)=x2-1 D. 1-a2=(1+a)(1-a)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于第一象限C,D两点,坐标轴交于A、B两点,连结OC,OD(O是坐标原点).
的图象交于第一象限C,D两点,坐标轴交于A、B两点,连结OC,OD(O是坐标原点).
(1)利用图中条件,求反比例函数的解析式和m的值;
(2)求△DOC的面积.
(3)双曲线上是否存在一点P,使得△POC和△POD的面积相等?若存在,给出证明并求出点P的坐标;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车匀速通过某段公路,所需时间t(h)与行驶速度v(km/h)满足函数关系:
t=![]() ,其图象为如图所示的一段曲线且端点为A(40,1)和B(m,0.5).
,其图象为如图所示的一段曲线且端点为A(40,1)和B(m,0.5).
(1)求k和m的值;(2)若行驶速度不得超过60 km/h,则汽车通过该路段最少需要多少时间?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com