
【题目】已知△ABC和△ADE都是等腰直角三角形,点D是直线BC上的一动点(点D不与B、C重合),连接CE.
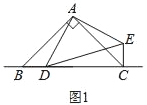
(1)在图1中,当点D在边BC上时,求证:BC=CE+CD;
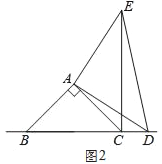
(2)在图2中,当点D在边BC的延长线上时,结论BC=CE+CD是否还成立?若不成立,请猜想BC、CE、CD之间存在的数量关系,并说明理由;
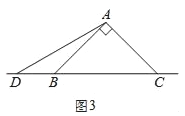
(3)在图3中,当点D在边BC的反向延长线上时,补全图形,不需写证明过程,直接写出BC、CE、CD之间存在的数量关系.
【答案】(1)见解析;(2)不成立,存在的数量关系为CE=BC+CD.理由见解析;(3)结论:CD=BC+EC.
【解析】
(1)在△ABD和△ACE中,由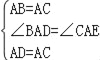 ,得△ABD≌△ACE(SAS),所以,BD=CE,
,得△ABD≌△ACE(SAS),所以,BD=CE,
可得BC=BD+CD=CE+CD;
(2)不成立,存在的数量关系为CE=BC+CD.同(1)△ABD≌△ACE(SAS),得BD=CE,所以BD=BC+CD,即CE=BC+CD;
(3)同(1)证△ABD≌△ACE(SAS),得BD=CE,所以CD=BC+BD=BC+CE.
(1)如图1中,
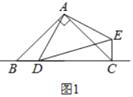
∵AB=AC,∠ABC=∠ACB=45°,AD=AE,∠ADE=∠AED=45°,
∴∠BAC=∠DAE=90°,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
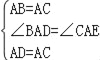 ,
,
∴△ABD≌△ACE(SAS),
∴BD=CE,
∴BC=BD+CD=CE+CD;
(2)不成立,存在的数量关系为CE=BC+CD.
理由:如图2,由(1)同理可得,
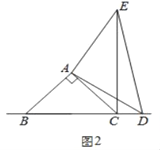
在△ABD和△ACE中,
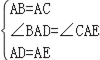 ,
,
∴△ABD≌△ACE(SAS),
∴BD=CE,
∴BD=BC+CD,
∴CE=BC+CD;
(3)如图3,结论:CD=BC+EC.
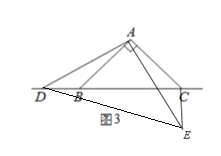
理由:由(1)同理可得,
在△ABD和△ACE中,
 ,
,
∴△ABD≌△ACE(SAS),
∴BD=CE,
∴CD=BC+BD=BC+CE,


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】以直线AB上一点O为端点作射线 OC,使∠BOC=60°,将一个直角三角形的直角顶点放在点O处.(注:∠DOE=90°)
(1)如图1,若直角三角板DOE的一边OD放在射线OB上,则∠COE= °;
(2)如图2,将直角三角板DOE绕点O逆时针方向转动到某个位置,若OE恰好平分∠AOC,请说明OD所在射线是∠BOC的平分线;
(3)如图3,将三角板DOE绕点O逆时针转动到某个位置时,若恰好∠COD= ![]() ∠AOE,求∠BOD的度数?
∠AOE,求∠BOD的度数?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC=AD.

(1)作∠A的平分线交CD于E;
(2)过B作CD的垂线,垂足为F;
(3)请写出图中两对全等三角形(不添加任何字母),并选择其中一对加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
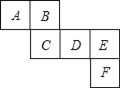
【题目】如图是一个正方体的表面展开图,请回答下列问题:
(1)与面B、C相对的面分别是 ;
(2)若A=a3+a2b+3,B=a2b﹣3,C=a3﹣1,D=﹣(a2b﹣6),且相对两个面所表示的代数式的和都相等,求E、F分别代表的代数式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:把代数式x2﹣6x﹣7因式分解,可以如下分解:
x2﹣6x﹣7
=x2﹣6x+9﹣9﹣7
=(x﹣3)2﹣16
=(x﹣3+4)(x﹣3﹣4)
=(x+1)(x﹣7)
(1)探究:请你仿照上面的方法,把代数式x2﹣8x+7因式分解;
(2)拓展:把代数式x2+2xy﹣3y2因式分解:
当![]() ________________时,代数式x2+2xy﹣3y2=0.
________________时,代数式x2+2xy﹣3y2=0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】上午8时,一条船从海岛A出发,以15海里/时的速度向正北航行,10时到达海岛B处,从A、B望灯塔C,测得∠BAC=60°,点C在点B的正西方向,海岛B与灯塔C之间的距离是_____海里.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=30°,点P是它内部一点,OP=2,如果点Q、点R分别是OA、OB上的两个动点,那么PQ+QR+RP的最小值是__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某景区的环形游览路线ABCDA,已知从景点C到出口A的两条道路CBA和CDA均为1600米,现有1号、2号两游览车分别从出口A和景点C同时出发,1号车顺时针、2号车逆时针沿环形道路连续循环行驶,供游客随时免费乘车(上、下车的时间忽略不计),两车的速度均为200米/分,每一个游客的步行速度均为50米/分.

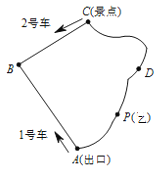

(1)探究(填空):
①当两车行驶 分钟时,1、2号车第一次相遇,此相遇点到出口A的路程为 米;
②当1号车第二次恰好经过点C,此时两车行驶了 分钟,这一段时间内1号车与2号车相遇了 次.
(2)发现:
若游客甲在BC上K处(不与点C、B重合)候车,准备乘车到出口A,在下面两种情况下,请问哪种情况用时较少(含候车时间)?请说明理由.
情况一:若他刚好错过2号车,便搭乘即将到来的1号车;
情况二:若他刚好错过1号车,便搭乘即将到来的2号车.
(3)决策:
①若游客乙在DA上从D向出口A走去,游客乙从D出发时恰好2号车在C处,当步行到DA上一点P(不与A,D重合)时,刚好与2号车相遇,经计算他发现:此时原地(P点)等候乘1号车到出口与直接从P步行到达出口A这两种方式,所花时间相等,请求出D点到出口A的路程.
②当游客丙逛完景点C后准备到出口A,此时2号车刚好在B点,已知BC路程为600米,请你帮助游客丙做一下决策,怎样到出口A所花时间最少,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com