
【题目】如图,在正方形ABCD中,E、F是对角线BD上两点,且∠EAF=45°,将△ADF绕点A顺时针旋转90°后,得到△ABQ,连接EQ,求证: 
(1)EA是∠QED的平分线;
(2)EF2=BE2+DF2 .
【答案】
(1)证明:∵将△ADF绕点A顺时针旋转90°后,得到△ABQ,
∴∠QAF=90°,
∵∠EAF=45°,
∴∠QAE=45°,
∴EA是∠QED的平分线
(2)证明:∵将△ADF绕点A顺时针旋转90°后,得到△ABQ,
∴QB=DF,AQ=AF,∠ABQ=∠ADF=45°,
在△AQE和△AFE中
 ,
,
∴△AQE≌△AFE(SAS),
∴QE=EF,
在Rt△QBE中,
QB2+BE2=QE2,
则EF2=BE2+DF2.

【解析】(1)直接利用旋转的性质得出对应线段关系进而得出答案;(2)直接利用旋转的性质得出△AQE≌△AFE(SAS),进而利用勾股定理得出答案.此题主要考查了旋转的性质以及全等三角形的判定与性质和勾股定理等知识,正确得出△AQE≌△AFE(SAS)是解题关键.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,∠ACB=90°,AC=BC,CD为AB边上的中线,点E、F分别在AC、BC边上,且ED⊥DF.
(1)求证:△CDE≌△BDF;
(2)如图2,作EG⊥AB于G,FH⊥AB于H,求证:EG+FH=CD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P为平行四边形ABCD边AD上一点,E、F分别是PB、PC(靠近点P)的三等分点,△PEF、△PDC、△PAB的面积分别为S1、S2、S3 , 若AD=2,AB=2 ![]() ,∠A=60°,则S1+S2+S3的值为( )
,∠A=60°,则S1+S2+S3的值为( ) 
A.![]()
B.![]()
C.![]()
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某图书馆开展两种方式的租书业务:一种是使用会员卡,另一种是使用租书卡,使用这两种卡租书,租书金额y(元)与租书时间x(天)之间的关系如下图所示。
(1)分别写出用租书卡和会员卡租书的金额y(元)与租书时间x(天)之间的函数关系式;
(2)两种租书方式,选取那种比较合适?说明理由

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在四边形ABCD中,E、F、G、H分别是BC、AD、BD、AC的中点.
①求证:EF与GH互相平分;
②当四边形ABCD的边满足______ 条件时,EF⊥GH.并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形 ABCD 的对角线 AC 与 BD 相交于点 O,CE∥BD, DE∥AC , AD=2![]() , DE=2,则四边形 OCED 的面积为( )
, DE=2,则四边形 OCED 的面积为( )

A. 2![]() B. 4 C. 4
B. 4 C. 4![]() D. 8
D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,![]() ,设c为最长边.当
,设c为最长边.当![]() 时,△ABC是直角三角形;当
时,△ABC是直角三角形;当![]() 时,利用代数式
时,利用代数式![]() 和
和![]() 的大小关系,可以判断△ABC的形状(按角分类).
的大小关系,可以判断△ABC的形状(按角分类).
(1)请你通过画图探究并判断:当△ABC三边长分别为6,8,9时,△ABC为____三角形;当△ABC三边长分别为6,8,11时,△ABC为______三角形.
(2)小明同学根据上述探究,有下面的猜想:“当![]() 时,△ABC为锐角三角形;当
时,△ABC为锐角三角形;当![]() 时,△ABC为钝角三角形.” 请你根据小明的猜想完成下面的问题:
时,△ABC为钝角三角形.” 请你根据小明的猜想完成下面的问题:
当![]() ,
,![]() 时,最长边c在什么范围内取值时,△ABC是直角三角形、锐角三角形、钝角三角形?
时,最长边c在什么范围内取值时,△ABC是直角三角形、锐角三角形、钝角三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是
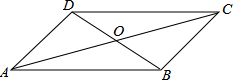
A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com