
【题目】如图,抛物线y=ax2+bx+c交x轴于A(﹣4,0),B(1,0),交y轴于C点,且OC=2OB.
(1)求抛物线的解析式;
(2)在直线BC上找点D,使△ABD为以AB为腰的等腰三角形,求D点的坐标.
(3)在抛物线上是否存在异于B的点P,过P点作PQ⊥AC于Q,使△APQ与△ABC相似?若存在,请求出P点坐标;若不存在,请说明理由.
【答案】
(1)解:∵B(1,0),OC=2OB,
∴C(0,﹣2),
设抛物线解析式为y=a(x+4)(x﹣1),
把C(0,﹣2)代入得a4(﹣1)=﹣2,解得a= ![]() ,
,
∴抛物线的解析式为y= ![]() (x+4)(x﹣1),即y=
(x+4)(x﹣1),即y= ![]() x2+
x2+ ![]() x﹣2
x﹣2
(2)解:AB=1﹣(﹣4)=5,
设直线BC的解析式为:y=kx+b,
把B(1,0),C(0,﹣2)代入得 ![]() ,解得
,解得 ![]() ,
,
∴直线BC的解析式为y=2x﹣2,
设D(m,2m﹣2),
∵△ABD为以AB为腰的等腰三角形,
∴BD=BA=5或AD=AB=5,
当BD=BA时,即(m﹣1)2+(2m﹣2)2=52,解得m1=1+ ![]() ,m2=1﹣
,m2=1﹣ ![]() ,此时D点坐标为(1+
,此时D点坐标为(1+ ![]() ,2
,2 ![]() ),(1﹣
),(1﹣ ![]() ,﹣2
,﹣2 ![]() ),
),
当AD=AB时,即(m+4)2+(2m﹣2)2=52,解得m1=1(舍去),m2=﹣1,此时D点坐标为(﹣1,﹣4),
综上所述,满足条件的D点坐标为(1+ ![]() ,2
,2 ![]() ),(1﹣
),(1﹣ ![]() ,﹣2
,﹣2 ![]() ),(﹣1,﹣4)
),(﹣1,﹣4)
(3)解:AB2=25,BC2=12+22=5,AC2=42+22=20,
∵AB2=BC2+AC2,
∴△ABC为直角三角形,∠ACB=90°,
∵∠BAC=∠CAO,
∴△ACO∽△ABC,
∵△APQ与△ABC相似,
∴∠CAP=∠OAC,
∴AC平分∠BAP,
设直线AP交y轴于E,作CF⊥AE于F,
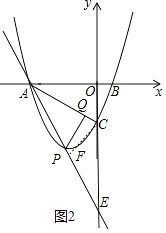
则CF=CO=2,
∵∠CEF=∠AEO,
∴△ECF∽△EAO,
∴ ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
在Rt△AOE中,∵OE2+OA2=AE2,
∴(2+CE)2+42![]() ,
,
∴E(0,﹣ ![]() ),
),
设直线AE的解析式为y=mx+n,
把A(﹣4,0),E(0,﹣ ![]() )得
)得 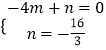 ,解得
,解得 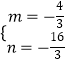 ,
,
∴直线AE的解析式为y=﹣ ![]() x﹣
x﹣ ![]() ,
,
解方程组 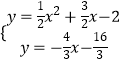 ,解得
,解得 ![]() 或
或 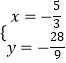 ,
,
∴P(﹣ ![]() ,﹣
,﹣ ![]() ).
).
【解析】根据OC=2OB.及点B的坐标就可以求出点C的坐标,注意:点C在y轴的负半轴,A、B两点坐标是此抛物线与x轴的两交点坐标,因此设函数解析式为两根式,代入点的坐标即可求出此抛物线的函数解析式。
(2)先求出AB的长及直线BC的函数解析式,抓住点D在直线BC上,设出点D的坐标,是以AB为腰的等腰三角形。再分类讨论。当BD=BA时和当AD=AB时,建立方程求解,即可求出满足条件的点D的坐标。
(3)要求点p的坐标,点P是直线AP与抛物线的交点坐标,解决此题的关键就是要求出直线AP的函数解析式。因此设直线AP交y轴于E,作CF⊥AE于F,,求出点E的坐标即可。根据已知条件易得到 △ ABC是直角三角形,从而得到△ACO∽△ABC,由△APQ与△ABC相似,得出AC平分∠BAP。根据角平分线的性质,得到CF=CO,再证明△ECF∽△EAO,求出CE和AE的数量关系,根据勾股定理就可以求出CE的长,即可得到点E的坐标,即可求出直线AE的解析式,再求出两函数图像的交点坐标即可得出结果。
【考点精析】解答此题的关键在于理解确定一次函数的表达式的相关知识,掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法,以及对勾股定理的概念的理解,了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:
【题目】若(x2+3mx﹣![]() )(x2﹣3x+n)的积中不含x和x3项,
)(x2﹣3x+n)的积中不含x和x3项,
(1)求m2﹣mn+![]() n2的值;
n2的值;
(2)求代数式(﹣18m2n)2+(9mn)﹣2+(3m)2014n2016的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AE⊥BD,CF⊥BD,E,F分别为垂足.
(1)求证:四边形AECF是平行四边形;
(2)如果AE=3,EF=4,求AF、EC所在直线的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年1月20日,山西迎来了“复兴号”列车,与“和谐号”相比,“复兴号”列车时速更快,安全性更好.已知“太原南﹣北京西”全程大约500千米,“复兴号”G92次列车平均每小时比某列“和谐号”列车多行驶40千米,其行驶时间是该列“和谐号”列车行驶时间的![]() (两列车中途停留时间均除外).经查询,“复兴号”G92次列车从太原南到北京西,中途只有石家庄一站,停留10分钟.求乘坐“复兴号”G92次列车从太原南到北京西需要多长时间.
(两列车中途停留时间均除外).经查询,“复兴号”G92次列车从太原南到北京西,中途只有石家庄一站,停留10分钟.求乘坐“复兴号”G92次列车从太原南到北京西需要多长时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在甲村至乙村的公路上有一块山地正在开发,现有一![]() 处需要爆破.已知点
处需要爆破.已知点![]() 与公路上的停靠站
与公路上的停靠站![]() 的距离为300米,与公路上的另一停靠站
的距离为300米,与公路上的另一停靠站![]() 的距离为400米,且
的距离为400米,且![]() ,如图所示为了安全起见,爆破点
,如图所示为了安全起见,爆破点![]() 周围半径250米范围内不得进入,问在进行爆破时,公路
周围半径250米范围内不得进入,问在进行爆破时,公路![]() 段是否因为有危险而需要暂时封锁?请说明理由.
段是否因为有危险而需要暂时封锁?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:某校一块长为2a米的正方形空地是七年级四个班的清洁区,其中分给七年级(1)班的清洁区是一块边长为(a-2b)米的正方形,(0<b<![]() ).
).
(1)分别求出七(2)、七(3)班的清洁区的面积;
(2)七(4)班的清洁区的面积比七(1)班的清洁区的面积多多少平方米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,对于点
中,对于点![]() ,若点
,若点![]() 的坐标为
的坐标为![]() ,则称点
,则称点![]() 是点
是点![]() 的“
的“![]() 演化点”.例如,点
演化点”.例如,点![]() 的“
的“![]() 演化点”为
演化点”为![]() ,即
,即![]() .
.
(1)已知点![]() 的“
的“![]() 演化点”是
演化点”是![]() ,则
,则![]() 的坐标为________;
的坐标为________;
(2)已知点![]() ,且点
,且点![]() 的“
的“![]() 演化点”是
演化点”是![]() ,则
,则![]() 的面积
的面积![]() 为__________;
为__________;
(3)己知![]() ,
,![]() ,
,![]() ,
,![]() ,且点
,且点![]() 的“
的“![]() 演化点”为
演化点”为![]() ,当
,当![]() 时,
时,![]() ___________.
___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 中,
中,![]() 厘米,
厘米,![]() ,
,![]() 厘米,点D为AB的中点
厘米,点D为AB的中点![]() 如果点P在线段BC上以v厘米
如果点P在线段BC上以v厘米![]() 秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动
秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动![]() 若点Q的运动速度为3厘米
若点Q的运动速度为3厘米![]() 秒,则当
秒,则当![]() 与
与![]() 全等时,v的值为
全等时,v的值为![]()
![]()

A. ![]() B. 3 C.
B. 3 C. ![]() 或3 D. 1或5
或3 D. 1或5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com