
【题目】在平面直角坐标系![]() 中,对于点
中,对于点![]() ,若点
,若点![]() 的坐标为
的坐标为![]() ,则称点
,则称点![]() 是点
是点![]() 的“
的“![]() 演化点”.例如,点
演化点”.例如,点![]() 的“
的“![]() 演化点”为
演化点”为![]() ,即
,即![]() .
.
(1)已知点![]() 的“
的“![]() 演化点”是
演化点”是![]() ,则
,则![]() 的坐标为________;
的坐标为________;
(2)已知点![]() ,且点
,且点![]() 的“
的“![]() 演化点”是
演化点”是![]() ,则
,则![]() 的面积
的面积![]() 为__________;
为__________;
(3)己知![]() ,
,![]() ,
,![]() ,
,![]() ,且点
,且点![]() 的“
的“![]() 演化点”为
演化点”为![]() ,当
,当![]() 时,
时,![]() ___________.
___________.
【答案】(2,14) 20 ![]()
【解析】
(1)根据题意a=3,x=-1,y=5时,求点![]() 的坐标;
的坐标;
(2)根据题意列方程组求点Q的坐标,然后结合坐标系中点的位置,利用割补法求三角形面积;
(3)根据题意求出![]() ,然后分点
,然后分点![]() 在y轴正半轴和负半轴两种情况讨论,利用三角形面积列方程求解.
在y轴正半轴和负半轴两种情况讨论,利用三角形面积列方程求解.
解:(1)由题意可知:点![]() 的“
的“![]() 演化点”是
演化点”是![]() ,即
,即![]() ,
,
故答案为:(2,14)
(2)设Q点坐标为(x,y),由题意可知:![]() ,解得:
,解得:![]()
∴Q点坐标为(0,4)
∴![]()
故答案为:20;
(3)由题意可知:AD=3,OC=5
![]() 的坐标为
的坐标为![]() ,即点
,即点![]() 的坐标为
的坐标为![]()
当点![]() 位于y轴正半轴时,
位于y轴正半轴时,![]() ,
,
∴![]() 或
或![]() (此情况不合题意,舍去)
(此情况不合题意,舍去)
又∵![]()
∴![]() ,解得:
,解得:![]() (舍去)
(舍去)
当点![]() 位于y轴正半轴时,
位于y轴正半轴时,![]() ,
,
∴
又∵![]()
∴![]() ,解得:
,解得:![]() ,即
,即![]()
故答案为:![]() .
.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c交x轴于A(﹣4,0),B(1,0),交y轴于C点,且OC=2OB.
(1)求抛物线的解析式;
(2)在直线BC上找点D,使△ABD为以AB为腰的等腰三角形,求D点的坐标.
(3)在抛物线上是否存在异于B的点P,过P点作PQ⊥AC于Q,使△APQ与△ABC相似?若存在,请求出P点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BC是⊙O的直径,A是⊙O上一点,过点C作⊙O的切线,交BA的延长线于点D,取CD的中点E,AE的延长线与BC的延长线交于点P.
(1)说明:AP是⊙O的切线;
(2)若OC=CP,AB=6,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2016年我县中小学经典诵读比赛中,10个参赛单位成绩统计如图所示,对于这10个参赛单位的成绩,下列说法中错误的是( )
A.众数是90
B.平均数是90
C.中位数是90
D.极差是15
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,BC=AC,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.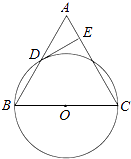
(1)求证:点D是AB的中点;
(2)判断DE与⊙O的位置关系,并证明你的结论;
(3)若⊙O的直径为18,cosB= ![]() ,求DE的长.
,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用锤子以相同的力将铁钉垂直钉入木块,随着铁钉的深入,铁钉所受的阻力也越来越大.当铁钉未进入木块部分长度足够时,每次钉入木块的铁钉长度是前一次的![]() ,已知这个铁钉被敲击3次后全部进入木块(木块足够厚),且第一次敲击后,铁钉进入木块的长度是a cm,若铁钉总长度为6cm,则a的取值范围是_______.
,已知这个铁钉被敲击3次后全部进入木块(木块足够厚),且第一次敲击后,铁钉进入木块的长度是a cm,若铁钉总长度为6cm,则a的取值范围是_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E是对角线BD上的一点,过点C作CF∥DB,且CF=DE,连接AE,BF,EF.
(1)求证:△ADE≌△BCF;
(2)若∠ABE+∠BFC=180°,则四边形ABFE是什么特殊四边形?说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,每个小正方形的边长为一个单位长度.已知△ABC的顶点A(-2,5)、B(-4,1)、C(2,3),将△ABC平移得到△A′B′C′,点A(a,b)对应点A′(a+3,b-4)
(1) 画出△A′B′C′并写出点B′、C′的坐标
(2) 试求线段AB在整个平移的过程中在坐标平面上扫过的面积
(3) 在x轴上存在一点P,使得S△ABP=6,则点P的坐标是_____________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com