

分析 首先判断出字母Q,N处的数字是奇数,字母P,M处的数字是偶数,可得2015这个数不在字母P,M处;然后判断出字母Q,N处的数字的排列规律,即可判断出2015这个数应排的位置.
解答 解:∵字母Q,N处的数字是奇数,字母P,M处的数字是偶数,
∴2015这个数不在字母P,M处;
∵3=4×1-1,7=4×2-1,11=4×3-1,…,
∴字母Q处的数字为:4n-1;
∵5=4×1+1,9=4×2+1,13=4×3+1,…,
∴字母N处的数字为:4n+1;
∵2015=4×504-1,
∴2015这个数应排的位置是Q.
故答案为:Q.
点评 此题主要考查了探寻数列规律问题,认真观察、仔细思考,善用联想是解决这类问题的方法,注意观察总结规律,并能正确的应用规律,解答此题的关键是判断出字母Q,N处的数字的排列规律.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
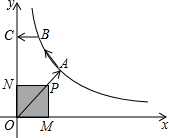 如图,已知A、B是反比例函数y=$\frac{k}{x}$(k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C,动点P纵坐标原点O出发,沿O→A→B→C匀速运动,终点为C,过点P作PM⊥x轴,PN⊥y轴,垂足分别为M、N.设四边形OMPN的面积为S,点P运动的时间为t,则S关于t的函数图象大致为( )
如图,已知A、B是反比例函数y=$\frac{k}{x}$(k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C,动点P纵坐标原点O出发,沿O→A→B→C匀速运动,终点为C,过点P作PM⊥x轴,PN⊥y轴,垂足分别为M、N.设四边形OMPN的面积为S,点P运动的时间为t,则S关于t的函数图象大致为( )| A. | 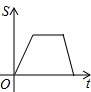 | B. | 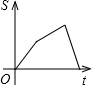 | C. | 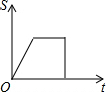 | D. | 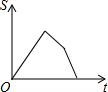 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
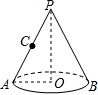 小明在圣诞节前做了一顶圆锥形纸帽PAB(如图),底面周长=14πcm,母线PA=28cm,一根彩带从母线PA的中点C开始绕圆锥形纸帽PAB的侧面到A点,则彩带长至少需14$\sqrt{5}$cm.
小明在圣诞节前做了一顶圆锥形纸帽PAB(如图),底面周长=14πcm,母线PA=28cm,一根彩带从母线PA的中点C开始绕圆锥形纸帽PAB的侧面到A点,则彩带长至少需14$\sqrt{5}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
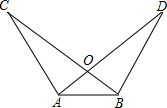 如图,已知AC=BD,∠C=∠D,试说明AD=BC,小丽的说理过程如下:
如图,已知AC=BD,∠C=∠D,试说明AD=BC,小丽的说理过程如下:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com