
【题目】星期天,小强骑自行车到效外与同学一起游玩.从家出发2小时到达目的地,游玩3小时后按原路以原速返回,小强离家4小时40分钟后,妈妈驾车沿相同路线迎接小强,如图是他们离家的路程y(千米)与时间x(时)的函数图象.已知小强骑车的速度为15千米/时,妈妈驾车的速度为60千米/时.
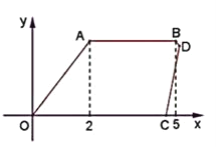
(1)小强家与游玩地的距离是多少?
(2)妈妈出发多长时间与小强相遇?
【答案】(1)30千米;(2) ![]() 小时(或28分钟)
小时(或28分钟)
【解析】
(1)利用路程=速度×时间计算即可;
(2)先利用待定系数法分别求出直线CD、BD的解析式,联立方程组即可求得交点横坐标,即为相遇的时间,减去妈妈出发时小强离家的时间即为所求.
解:(1)小强家与游玩地的距离是15×2=30,
即小强家与游玩地的距离为30千米;
(2)∵小强骑车的速度为15千米/时,妈妈驾车的速度为60千米/时.
∴设yOA=15x,yBD=﹣15x+b1,yCD=60x+b2,
∵点B(5,30),点C(![]() ,0),
,0),
则30=﹣15×5+b1,
解得b1=105,
0=60×![]() +b2,
+b2,
解得b2=﹣280,
则yBD=﹣15x+105,yCD=60x﹣280,相遇即为﹣15x+105=60x﹣280,
解得x=5![]() ,
,
5![]() ﹣4
﹣4![]() =
=![]() 小时(即28分钟).
小时(即28分钟).
或设妈妈出发x时间与小强相遇,则
60x+15(x﹣![]() )=30,
)=30,
解得x=![]() (即28分钟).
(即28分钟).
即妈妈出发28分钟与小强相遇.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形ABCD的三个顶点A,B,D在坐标轴上,且已知点A(![]() ,
,![]() ),点B(
),点B(![]() ,
,![]() ),现有抛物线m经过点B,C和OD的中点.
),现有抛物线m经过点B,C和OD的中点.
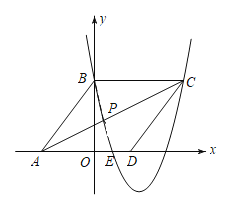
(1)求抛物线m的解析式;
(2)在抛物线![]() 上是否存在点P,使得
上是否存在点P,使得![]() ?若存在,求出点P的坐标,若不存在,请说明理由;
?若存在,求出点P的坐标,若不存在,请说明理由;
(3)抛物线m与x轴的另一交点为F,M是线段AC上一动点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形![]() 的顶点
的顶点![]() ,点
,点![]() ,反比例函数
,反比例函数![]()
(1)如图1,双曲线经过点![]() 时求反比例函数
时求反比例函数![]() 的关系式;
的关系式;
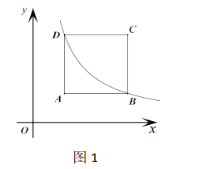
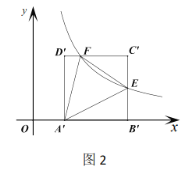
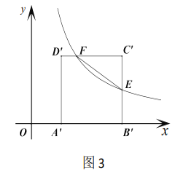
(2)如图2,正方形![]() 向下平移得到正方形
向下平移得到正方形![]() 边
边![]() 在
在![]() 轴上,反比例函数
轴上,反比例函数![]() 的图象分别交正方形
的图象分别交正方形![]() 的边
的边![]() 、边
、边![]() 于点
于点![]()
①求![]() 的面积;
的面积;
②如图3,![]() 轴上一点
轴上一点![]() ,是否存在
,是否存在![]() 是等腰三角形,若存在直接写出点
是等腰三角形,若存在直接写出点![]() 坐标,若不存在请说明理由.
坐标,若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班为推荐选手参加学校举办的“祖国在我心中”演讲比赛活动,先在班级中进行预赛,班主任根据学生的成绩从高到低划分为A,B,C,D四个等级,并绘制了不完整的两种统计图表.请根据图中提供的信息,回答下列问题:
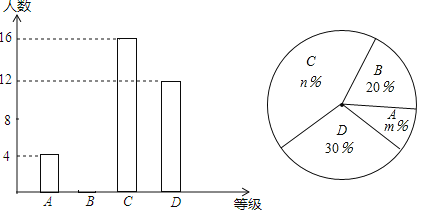
(1)a的值为 ;
(2)求C等级对应扇形的圆心角的度数;
(3)获得A等级的4名学生中恰好有1男3女,该班将从中随机选取2人,参加学校举办的演讲比赛,请利用列表法或画树状图法,求恰好选中一男一女参加比赛的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,AB=4,BC=2,正方形ADEF的边长为2,F、A、B在同一直线上,正方形ADEF向右平移到点F与B重合,点F的平移距离为x,平移过程中两图重叠部分的面积为y,则y与x的关系的函数图象表示正确的是( )
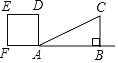
A.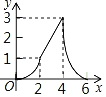 B.
B.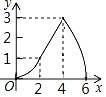
C.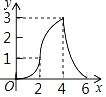 D.
D.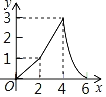
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣![]() x2+bx+c与x轴交于点A和点B,与y轴交于点C,点B坐标为(4,0),点C坐标为(0,4),点D是抛物线的顶点,过点D作x轴的垂线,垂足为E,连接BD.
x2+bx+c与x轴交于点A和点B,与y轴交于点C,点B坐标为(4,0),点C坐标为(0,4),点D是抛物线的顶点,过点D作x轴的垂线,垂足为E,连接BD.
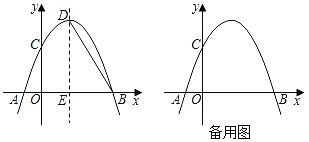
(1)求抛物线的解析式及点D的坐标;
(2)点F是抛物线上的动点,当∠FBA=2∠BDE时,求点F的坐标;
(3)若点P是x轴上方抛物线上的动点,以PB为边作正方形PBGH,随着点P的运动,正方形的大小、位置也随着改变,当顶点G或H恰好落在y轴上时,请直接写出点P的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017江西省)如图1,研究发现,科学使用电脑时,望向荧光屏幕画面的“视线角”α约为20°,而当手指接触键盘时,肘部形成的“手肘角”β约为100°.图2是其侧面简化示意图,其中视线AB水平,且与屏幕BC垂直.
(1)若屏幕上下宽BC=20cm,科学使用电脑时,求眼睛与屏幕的最短距离AB的长;
(2)若肩膀到水平地面的距离DG=100cm,上臂DE=30cm,下臂EF水平放置在键盘上,其到地面的距离FH=72cm.请判断此时β是否符合科学要求的100°?
(参考数据:sin69°≈![]() ,cos21°≈
,cos21°≈![]() ,tan20°≈
,tan20°≈![]() ,tan43°≈
,tan43°≈![]() ,所有结果精确到个位)
,所有结果精确到个位)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com