
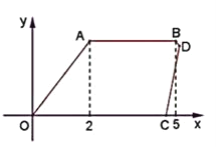
【题目】如图,在平面直角坐标系中,菱形ABCD的三个顶点A,B,D在坐标轴上,且已知点A(![]() ,
,![]() ),点B(
),点B(![]() ,
,![]() ),现有抛物线m经过点B,C和OD的中点.
),现有抛物线m经过点B,C和OD的中点.
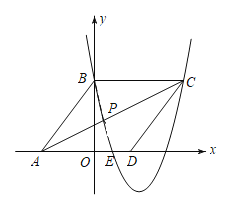
(1)求抛物线m的解析式;
(2)在抛物线![]() 上是否存在点P,使得
上是否存在点P,使得![]() ?若存在,求出点P的坐标,若不存在,请说明理由;
?若存在,求出点P的坐标,若不存在,请说明理由;
(3)抛物线m与x轴的另一交点为F,M是线段AC上一动点,求![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)存在满足条件的点
;(2)存在满足条件的点![]() ,使得
,使得![]() ,理由见解析;(3)
,理由见解析;(3)![]()
【解析】
(1)先求出点C和点D的坐标,再求出点E的坐标,设出函数m的解析式,把B、E、C三点坐标代入解析式进行求解即可;
(2)![]() 点是抛物线
点是抛物线![]() 和直线
和直线![]() 的交点,求出AC的解析式,联立方程组,解出方程组进行取舍即可得点P坐标;
的交点,求出AC的解析式,联立方程组,解出方程组进行取舍即可得点P坐标;
(3)过![]() 作
作![]() 轴于
轴于![]() ,过
,过![]() 作
作![]() 于
于![]() ,证明△AOG∽△CNM,可得
,证明△AOG∽△CNM,可得![]() ,从而可得结论.
,从而可得结论.
(1)∵![]() ,
,![]()
∴![]() ,
,![]()
∴![]() ,即菱形的长为5,
,即菱形的长为5,
∴![]() ,
,![]()
∴![]() ,
,![]()
∴OD的中点坐标为:![]()
设抛物线的解析式为:![]() ,则
,则
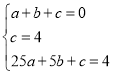 ,解得
,解得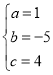
∴抛物线![]() 的解析式为
的解析式为![]() .
.
(2)存在满足条件的点![]() ,使得
,使得![]() .理由如下:
.理由如下:
①当点P在BC下方时,∵![]() ,
,![]() ,
,
∴![]() 点在菱形
点在菱形![]() 的对角线上,
的对角线上,
∴![]() 点是抛物线
点是抛物线![]() 和直线
和直线![]() 的交点,
的交点,
设直线![]() 的解析式为
的解析式为![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,解得
,解得![]() ,
,
∴直线![]() 的解析式为
的解析式为![]() ,
,
由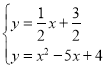 解得
解得![]() 或
或![]() (舍去),
(舍去),
∴![]() ,
,![]() .
.
(3)过![]() 作
作![]() 轴于
轴于![]() ,过
,过![]() 作
作![]() 于
于![]() ,
,
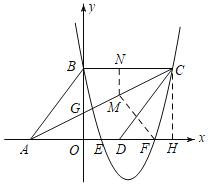
∵![]() 轴,∴
轴,∴![]() ,
,
又∵![]() ,
,
∴△AOG∽△CNM,
∴![]() ,
,
∴![]() ,
,
∵点![]() 到
到![]() 最小距离为
最小距离为![]() ,
,
∴![]() 的最小值为
的最小值为![]() 的长度4,
的长度4,
∴![]() 的最小值为
的最小值为![]() .
.


科目:初中数学 来源: 题型:
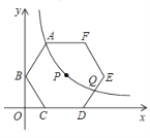
【题目】如图,在平面直角坐标系中,正六边形![]() 的对称中心
的对称中心![]() 在反比例函数
在反比例函数![]() 的图象上,边
的图象上,边![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上,已知
轴上,已知![]() .若该反比例函数图象与
.若该反比例函数图象与![]() 交于点
交于点![]() ,则点的
,则点的![]() 横坐标是_________.
横坐标是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
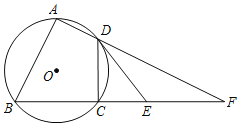
【题目】如图,四边形ABCD内接于⊙O,AB=AC,∠BAD=90°,延长AD,BC交于点F.过点D作⊙O的切线,交BF于点E.
(1)求证:DE=EF;
(2)若![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市以20元/kg的价格购进一批商品进行销售,根据以往的销售经验及对市场行情的调研,该超市得到日销售量y(kg)与销售价格x(元/kg)之间的关系,部分数据如下表:
销售价格x(元/kg) | 25 | 30 | 35 | 40 | … |
日销售量y(kg) | 1000 | 800 | 600 | 400 | … |
(1)根据表中的数据,用所学过的函数知识确定y与x之间的函数关系式;
(2)超市应如何确定销售价格,才能使日销售利润W(元)最大?W最大值为多少?
(3)供货商为了促销,决定给予超市a元/kg的补贴,但希望超市在30≤x≤35时,最大利润不超过10240元,求a的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
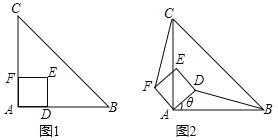
【题目】(1)问题发现:如图1,△ABC是等腰直角三角形,四边形ADEF是正方形,点D、F分别在边AB、AC上,请直接写出线段BD、CF的数量和位置关系;
(2)拓展探究:如图2,当正方形ADEF绕点A逆时针旋转锐角θ时,上述结论还成立吗?若成立,请给予证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C在⊙O上,点D在AB的延长线上,且∠BCD![]() ∠A.
∠A.
(1)求证:CD是⊙O的切线;
(2)若AC![]() 2,AB
2,AB![]()
![]() CD,求⊙O半径.
CD,求⊙O半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着新冠病毒在全世界蔓延,口罩成为紧缺物资,甲、乙两家工厂积极响应政府号召,准备跨界投资生产口罩.根据市场调查,甲、乙两家工厂计划每天各生产6万片口罩,但由于转型条件不同,其生产的成本不一样,甲工厂计划每生产1万片口罩的成本为0.6万元,乙工厂计划每生产1万片口罩的成本为0.8万元.
(1)按照计划,甲、乙两家工厂共生产2000万片口罩,且甲工厂生产口罩的总成本不高于乙工厂生产口罩的总成本的![]() ,求甲工厂最多可生产多少万片的口罩?
,求甲工厂最多可生产多少万片的口罩?
(2)实际生产时,甲工厂完全按计划执行,但乙工厂的生产情况发生了一些变化.乙工厂实际每天比计划少生产0.5m万片口罩,每生产1万片口罩的成本比计划多0.2m万元,最终乙工厂实际每天生产口罩的成本比计划多1.6万元,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于![]() 的一次函数
的一次函数![]() 和反比例函数
和反比例函数![]() 的图像都经过点
的图像都经过点![]() .
.
求:(1)一次函数和反比例函数的解析式;
(2)若一次函数和反比例函数图像的另一个交点![]() 的坐标为
的坐标为![]() ,请结合图像直接写出
,请结合图像直接写出![]() 的
的![]() 取值范围.
取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】星期天,小强骑自行车到效外与同学一起游玩.从家出发2小时到达目的地,游玩3小时后按原路以原速返回,小强离家4小时40分钟后,妈妈驾车沿相同路线迎接小强,如图是他们离家的路程y(千米)与时间x(时)的函数图象.已知小强骑车的速度为15千米/时,妈妈驾车的速度为60千米/时.
(1)小强家与游玩地的距离是多少?
(2)妈妈出发多长时间与小强相遇?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com