
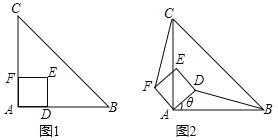
【题目】(1)问题发现:如图1,△ABC是等腰直角三角形,四边形ADEF是正方形,点D、F分别在边AB、AC上,请直接写出线段BD、CF的数量和位置关系;
(2)拓展探究:如图2,当正方形ADEF绕点A逆时针旋转锐角θ时,上述结论还成立吗?若成立,请给予证明;若不成立,请说明理由.
【答案】(1)BD=CF,BD⊥CF,理由见解析;(2)成立,理由见解析.
【解析】
(1)根据等腰直角三角形的性质和正方形的性质解答即可;
(2)△ABC是等腰直角三角形,四边形ADEF是正方形,易证得△BAD≌△CAF,根据全等三角形的对边相等,即可证得BD=CF,进而证明BD⊥CF
(1)BD=CF,BD⊥CF,理由如下:
∵△ABC是等腰直角三角形,四边形ADEF是正方形,
∴AB=AC,AD=AF,∠BAC=∠DAF=90°,
∴BD=CF,BD⊥CF;
(2)成立,理由如下:
∵△ABC是等腰直角三角形,四边形ADEF是正方形,
∴AB=AC,AD=AF,∠BAC=∠DAF=90°,
∵∠BAD=∠BAC﹣∠DAC,∠CAF=∠DAF﹣∠DAC,
∴∠BAD=∠CAF,
在△BAD与△CAF中,
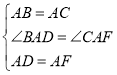 ,
,
∴△BAD≌△CAF(SAS),
∴BD=CF,
延长BD,分别交直线AC、CF于点M,G,如图,
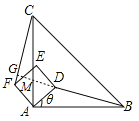
∵△BAD≌△CAF,
∴∠ABM=∠GCM,
∵∠BMA=∠CMG,
∴∠BGC=∠BAC=90°,
∴BD⊥CF.


科目:初中数学 来源: 题型:
【题目】2019年12月17日,我国第一艘国产航母“山东舰”在海南三亚交付海军.在民族复兴的路上我们伟大的祖国又前进了一大步!如图,“山东舰”在一次试水测试中,由东向西航行到达![]() 处时,测得小岛
处时,测得小岛![]() 位于距离航母30海里的北偏东37°方向.“山东舰”再向西匀速航行1.5小时后到达
位于距离航母30海里的北偏东37°方向.“山东舰”再向西匀速航行1.5小时后到达![]() 处,此时测得小岛
处,此时测得小岛![]() 位于航母的北偏东70°方向.
位于航母的北偏东70°方向.
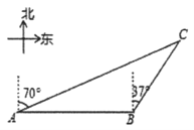
(1)![]() _______°;
_______°;
(2)求航母的速度.(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AD∥BC,AC平分∠BAD,∠ABC=60°,E为AD上一点,AE=2,DE=4,P为AC 上一点,则△PDE周长的最小值为_______.
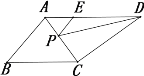
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 经过点A(-3,0),C(0,3),交x轴于另一点B,其顶点为D.
经过点A(-3,0),C(0,3),交x轴于另一点B,其顶点为D.
(1)求抛物线的解析式;
(2)点P为抛物线上一点,直线CP交x轴于点E,若△CAE与△OCD相似,求P点坐标;
(3)如果点F在y轴上,点M在直线AC上,那么在抛物线上是否存在点N,使得以C,F,M,N为顶点的四边形是菱形?若存在,请求出菱形的周长;若不存在,请说明理由.
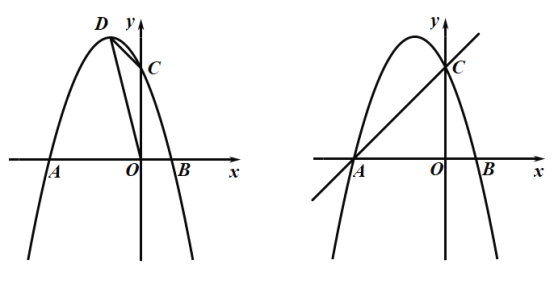
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形ABCD的三个顶点A,B,D在坐标轴上,且已知点A(![]() ,
,![]() ),点B(
),点B(![]() ,
,![]() ),现有抛物线m经过点B,C和OD的中点.
),现有抛物线m经过点B,C和OD的中点.
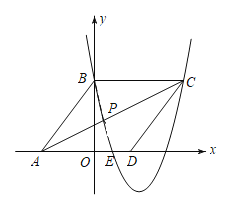
(1)求抛物线m的解析式;
(2)在抛物线![]() 上是否存在点P,使得
上是否存在点P,使得![]() ?若存在,求出点P的坐标,若不存在,请说明理由;
?若存在,求出点P的坐标,若不存在,请说明理由;
(3)抛物线m与x轴的另一交点为F,M是线段AC上一动点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC与△CDE中,∠ACB![]() ∠CDE
∠CDE![]() 90°,AC
90°,AC![]() BC,CD
BC,CD![]() ED,连接AE,BE,F为AE的中点,连接DF,△CDE绕着点C旋转.
ED,连接AE,BE,F为AE的中点,连接DF,△CDE绕着点C旋转.
(1)如图1,当点D落在AC上时,DF与BE的数量关系是: ;
(2)如图2,当△CDE旋转到该位置时,DF与BE是否仍具有(1)中的数量关系,如果具有,请给予证明;如果没有,请说明理由;
(3)如图3,当点E落在线段CB延长线上时,若CD![]() AC
AC![]() 2,求DF的长.
2,求DF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() ,直线
,直线![]() 与抛物线、
与抛物线、![]() 轴分别相交于
轴分别相交于![]() 、
、![]() .
.

(1)![]() 时,
时,![]() 点的坐标为________;
点的坐标为________;
(2)当![]() 、
、![]() 两点重合时,求
两点重合时,求![]() 的值;
的值;
(3)当![]() 点达到最高时,求抛物线解析式;
点达到最高时,求抛物线解析式;
(4)在抛物线![]() 与
与![]() 轴所围成的封闭图形的边界上,我们把横坐标是整数的点称为“可点”,直接写出
轴所围成的封闭图形的边界上,我们把横坐标是整数的点称为“可点”,直接写出![]() 时“可点”的个数为____.
时“可点”的个数为____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com