
【题目】在△ABC与△CDE中,∠ACB![]() ∠CDE
∠CDE![]() 90°,AC
90°,AC![]() BC,CD
BC,CD![]() ED,连接AE,BE,F为AE的中点,连接DF,△CDE绕着点C旋转.
ED,连接AE,BE,F为AE的中点,连接DF,△CDE绕着点C旋转.
(1)如图1,当点D落在AC上时,DF与BE的数量关系是: ;
(2)如图2,当△CDE旋转到该位置时,DF与BE是否仍具有(1)中的数量关系,如果具有,请给予证明;如果没有,请说明理由;
(3)如图3,当点E落在线段CB延长线上时,若CD![]() AC
AC![]() 2,求DF的长.
2,求DF的长.

【答案】(1)DF=![]() BE;(2)见解析;(3)
BE;(2)见解析;(3)![]() ;
;
【解析】
(1)证明△ACE≌△BCE,则AE=BE,DF是直角△ADE的中线,DF=![]() AE,即可证明DF=
AE,即可证明DF=![]() BE;
BE;
(2)连接AM,证明△ACM≌△BCE,则AM=BE,DF为△AME的中位线,DF=![]() =
=![]() BE;
BE;
(3)易知CD=DE=2,由勾股定理CE=![]() ,BE=CE—CB=
,BE=CE—CB=![]() ,DF=
,DF=![]() BE,可求得DF=
BE,可求得DF=![]() .
.
(1) ∵∠ACB=∠CDE=90°,AC=BC,CD =ED,
∴∠ACE=∠BCE=45°,
∴△ACE≌△BCE,
∴AE=BE,因为DF是直角△ADE的中线,
∴DF=![]() AE
AE
∴DF=![]() BE
BE
(2)如图,将△CDE沿着CD翻折,得到△DCM≌△DCE,连接AM,
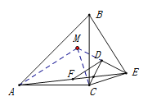
由△CDE为等腰直角三角形易知△CME为等腰直角三角形,
在△ACM和△BCE中,
AC=BC,∠ACM=∠BCE ,CM=CE,
∴△ACM≌△BCE,
∴AM=BE
∵F为AE的中点,D为ME的中点
∴DF为△AME的中位线,
∴DF=![]() ,
,
∴DF=![]() BE.
BE.
(3)将△EDC沿DC翻折得到△DCM
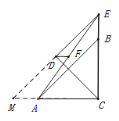
CD=DE=2,由勾股定理可知CE=![]()
BE=CE—CB=![]()
由前面的结论可知:DF=![]() BE
BE
∴DF=![]() .
.


科目:初中数学 来源: 题型:
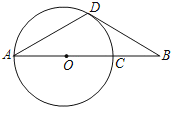
【题目】如图,线段AB经过⊙O的圆心O,交⊙O于A、C两点,BC=1,AD为⊙O的弦,连结BD,∠BAD=∠ABD=30°.
(1)求证:直线BD是⊙O的切线;
(2)求⊙O的半径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
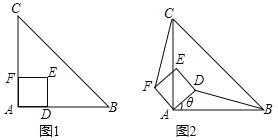
【题目】(1)问题发现:如图1,△ABC是等腰直角三角形,四边形ADEF是正方形,点D、F分别在边AB、AC上,请直接写出线段BD、CF的数量和位置关系;
(2)拓展探究:如图2,当正方形ADEF绕点A逆时针旋转锐角θ时,上述结论还成立吗?若成立,请给予证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
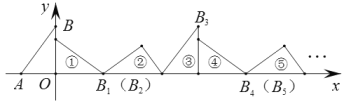
【题目】如图,在平面直角坐标系中,已知点A(-1.5,0),B(0,2),将△ABO顺着x轴的正半轴无滑动的滚动,第一次滚动到①的位置,点B的对应点记作B1;第二次滚动到②的位置,点B1的对应点记作B2;第三次滚动到③的位置,点B2的对应点记作B3;![]() ;依次进行下去,则点B2020的坐标为__________.
;依次进行下去,则点B2020的坐标为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着新冠病毒在全世界蔓延,口罩成为紧缺物资,甲、乙两家工厂积极响应政府号召,准备跨界投资生产口罩.根据市场调查,甲、乙两家工厂计划每天各生产6万片口罩,但由于转型条件不同,其生产的成本不一样,甲工厂计划每生产1万片口罩的成本为0.6万元,乙工厂计划每生产1万片口罩的成本为0.8万元.
(1)按照计划,甲、乙两家工厂共生产2000万片口罩,且甲工厂生产口罩的总成本不高于乙工厂生产口罩的总成本的![]() ,求甲工厂最多可生产多少万片的口罩?
,求甲工厂最多可生产多少万片的口罩?
(2)实际生产时,甲工厂完全按计划执行,但乙工厂的生产情况发生了一些变化.乙工厂实际每天比计划少生产0.5m万片口罩,每生产1万片口罩的成本比计划多0.2m万元,最终乙工厂实际每天生产口罩的成本比计划多1.6万元,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=﹣x2+2(m﹣2)x+3的图象与x、y轴交于A、B、C三点,其中A(3,0),抛物线的顶点为D.
(1)求m的值及顶点D的坐标;
(2)如图1,若动点P在第一象限内的抛物线上,动点N在对称轴1上,当PA⊥NA,且PA=NA时,求此时点P的坐标;
(3)如图2,若点Q是二次函数图象上对称轴右侧一点,设点Q到直线BC的距离为d,到抛物线的对称轴的距离为d1,当|d﹣d1|=2时,请求出点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接2022年冬奥会,鼓励更多的大学生参与到志愿服务中,甲、乙两所学校组织了志愿服务团队选拔活动,经过初选,两所学校各有300名学生进入综合素质展示环节,为了了解这些学生的整体情况,从两校进入综合素质展示环节的学生中分别随机抽取了50名学生的综合素质展示成绩(百分制),并对数据(成绩)进行整理、描述和分析,下面给出了部分信息.
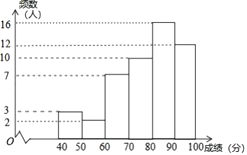
a.甲学校学生成绩的频数分布直方图如图(数据分成6组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ).
).
b.甲学校学生成绩在![]() 这一组是:
这一组是:
80 80 81 81.5 82 83 83 84
85 86 86.5 87 88 88.5 89 89
c.乙学校学生成绩的平均数、中位数、众数、优秀率(85分及以上为优秀)如下:
平均数 | 中位数 | 众数 | 优秀率 |
83.3 | 84 | 78 | 46% |
根据以上信息,回答下列问题:
(1)甲学校学生![]() ,乙学校学生
,乙学校学生![]() 的综合素质展示成绩同为82分,这两人在本校学生中综合素质展示排名更靠前的是________(填“
的综合素质展示成绩同为82分,这两人在本校学生中综合素质展示排名更靠前的是________(填“![]() ”或“
”或“![]() ”);
”);
(2)根据上述信息,推断________学校综合素质展示的水平更高,理由为:__________________________
(至少从两个不同的角度说明推断的合理性).
(3)若每所学校综合素质展示的前120名学生将被选入志愿服务团队,预估甲学校分数至少达到________分的学生才可以入选.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com