
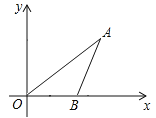
【题目】如图,已知点![]() 坐标为
坐标为![]() ,
,![]() 为
为![]() 轴正半轴上一动点,则
轴正半轴上一动点,则![]() 度数为_________,在点
度数为_________,在点![]() 运动的过程中
运动的过程中![]() 的最小值为________.
的最小值为________.
【答案】30° ![]()
【解析】
过点A作A关于x轴的对称点C,交x轴于点D,过点C作CM⊥OA于点M,交x轴于点B,根据A点坐标,写出AD和OD长,根据三角函数知识求出∠AOB即可,证BM=![]() ,AB=BC,得到
,AB=BC,得到![]() ,然后在Rt△ACM中,根据三角函数知识求出CM即可.
,然后在Rt△ACM中,根据三角函数知识求出CM即可.
解:过点A作A关于x轴的对称点C,交x轴于点D,过点C作CM⊥OA于点M,交x轴于点B,
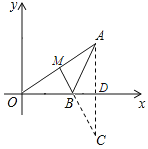
∵点![]() 坐标为
坐标为![]() ,AD⊥x轴,
,AD⊥x轴,
∴AD=1,OD=![]() ,
,
∴在Rt△AOD中,
![]() ,
,
∴∠AOB=30°;
∵CM⊥OA,
∴∠OMB=∠AMB=90°,
∴BM=![]() ,
,
∵∠OBM=∠DBC,
∴∠ACM=30°,
∵A,C关于x轴对称,
∴AB=BC,AD=CD=1,
∴AC=2,
∴![]() ,
,
∴当C,B,M三点共线时,![]() 有最小值,即CM长,
有最小值,即CM长,
在Rt△ACM中,
CM=![]() ,
,
故答案为:30°;![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,点E、F分别在边AB和CD上,下列条件不能判定四边形DEBF一定是平行四边形的是( )

A.AE=CFB.DE=BFC.∠ADE=∠CBFD.∠AED=∠CFB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,连接BD,点E在AB上,连接CE交BD于点F,作FG⊥BC于点G,∠BEC=3∠BCE,BF=![]() DF,若FG=
DF,若FG=![]() ,则AB的长为_____.
,则AB的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB 是⊙ O 的直径,点 C 是⊙ O 上的一点,点 D 是弧 BC 的中点,连接 AC, BD,过点 D 作 AC 的垂线 EF,交 AC 的延长线于点 E,交 AB 的延长线于点 F..

(1)依题意补全图形;
(2)判断直线 EF 与⊙ O 的位置关系,并说明理由
(3)若 AB=5,BD=3,求线段 BF 的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)“校园诗歌大赛”结束后,张老师和李老师将所有参赛选手的比赛成绩(得分均为整数)进行整理,并分别绘制成扇形统计图和频数直方图部分信息如下:
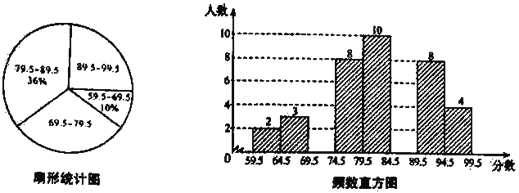
(1)本次比赛参赛选手共有 人,扇形统计图中“69.5~79.5”这一组人数占总参赛人数的百分比为 ;
(2)赛前规定,成绩由高到低前60%的参赛选手获奖.某参赛选手的比赛成绩为78分,试判断他能否获奖,并说明理由;
(3)成绩前四名是2名男生和2名女生,若从他们中任选2人作为获奖代表发言,试求恰好选中1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() ,直线
,直线![]() 与抛物线、
与抛物线、![]() 轴分别相交于
轴分别相交于![]() 、
、![]() .
.

(1)![]() 时,
时,![]() 点的坐标为________;
点的坐标为________;
(2)当![]() 、
、![]() 两点重合时,求
两点重合时,求![]() 的值;
的值;
(3)当![]() 点达到最高时,求抛物线解析式;
点达到最高时,求抛物线解析式;
(4)在抛物线![]() 与
与![]() 轴所围成的封闭图形的边界上,我们把横坐标是整数的点称为“可点”,直接写出
轴所围成的封闭图形的边界上,我们把横坐标是整数的点称为“可点”,直接写出![]() 时“可点”的个数为____.
时“可点”的个数为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 为
为![]() 边上一点,且
边上一点,且![]() .点
.点![]() 从点
从点![]() 出发.沿射线
出发.沿射线![]() 以每秒1个单位长度的速度运动.以
以每秒1个单位长度的速度运动.以![]() 、
、![]() 为邻边作
为邻边作![]() .设
.设![]() 和
和![]() 重叠部分图形的面积为
重叠部分图形的面积为![]() (平方单位),点
(平方单位),点![]() 的运动时间为
的运动时间为![]() (秒)
(秒)![]() .
.
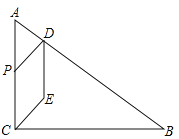
(1)连结![]() ,求
,求![]() 的长.
的长.
(2)当![]() 为菱形时,求
为菱形时,求![]() 的值.
的值.
(3)求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(4)将线段![]() 沿直线
沿直线![]() 翻折得到线段
翻折得到线段![]() .当点
.当点![]() 落在
落在![]() 的边上时,直接写出
的边上时,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 经过点
经过点![]() ,且抛物线上任意不同两点
,且抛物线上任意不同两点![]() 都满足:当
都满足:当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;抛物线与
;抛物线与![]() 轴另一个交点为
轴另一个交点为![]() ,与
,与![]() 轴交于
轴交于![]() 点,对称轴与
点,对称轴与![]() 轴交于
轴交于![]() 点.
点.
(1)求抛物线的对称轴及点![]() 的坐标;
的坐标;
(2)过点![]() 作
作![]() 轴的平行线交抛物线的对称轴于点
轴的平行线交抛物线的对称轴于点![]() ,当四边形
,当四边形![]() 是正方形时,求抛物线的解析式;
是正方形时,求抛物线的解析式;
(3)在(2)的条件下,垂直于![]() 轴的直线
轴的直线![]() 与抛物线交于点
与抛物线交于点![]() 和
和![]() ,与直线
,与直线![]() 交于点
交于点![]() ,若
,若![]() ,结合函数的图象,直接写出
,结合函数的图象,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
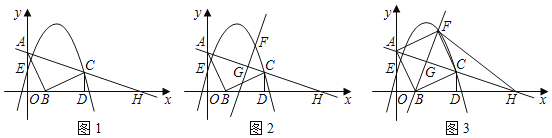
【题目】综合与探究:
如图1,![]() 的直角顶点
的直角顶点![]() 在坐标原点,点
在坐标原点,点![]() 在
在![]() 轴正半轴上,点
轴正半轴上,点![]() 在
在![]() 轴正半轴上,
轴正半轴上,![]() ,
,![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到线段
得到线段![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,抛物线
,抛物线![]() 经过点
经过点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
(1)求点![]() 的坐标及抛物线的表达式;
的坐标及抛物线的表达式;
(2)如图2,已知点![]() 是线段
是线段![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 的垂线交抛物线于点
的垂线交抛物线于点![]() (点
(点![]() 在第一象限),设点
在第一象限),设点![]() 的横坐标为
的横坐标为![]() .
.
①点![]() 的纵坐标用含
的纵坐标用含![]() 的代数式表示为________;
的代数式表示为________;
②如图3,当直线![]() 经过点
经过点![]() 时,求点
时,求点![]() 的坐标,判断四边形
的坐标,判断四边形![]() 的形状并证明结论;
的形状并证明结论;
③在②的前提下,连接![]() ,点
,点![]() 是坐标平面内的点,若以
是坐标平面内的点,若以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 全等,请直接写出点
全等,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com