
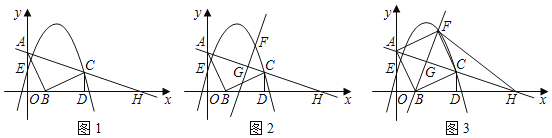
【题目】综合与探究:
如图1,![]() 的直角顶点
的直角顶点![]() 在坐标原点,点
在坐标原点,点![]() 在
在![]() 轴正半轴上,点
轴正半轴上,点![]() 在
在![]() 轴正半轴上,
轴正半轴上,![]() ,
,![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到线段
得到线段![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,抛物线
,抛物线![]() 经过点
经过点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
(1)求点![]() 的坐标及抛物线的表达式;
的坐标及抛物线的表达式;
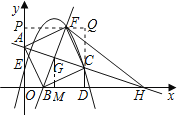
(2)如图2,已知点![]() 是线段
是线段![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 的垂线交抛物线于点
的垂线交抛物线于点![]() (点
(点![]() 在第一象限),设点
在第一象限),设点![]() 的横坐标为
的横坐标为![]() .
.
①点![]() 的纵坐标用含
的纵坐标用含![]() 的代数式表示为________;
的代数式表示为________;
②如图3,当直线![]() 经过点
经过点![]() 时,求点
时,求点![]() 的坐标,判断四边形
的坐标,判断四边形![]() 的形状并证明结论;
的形状并证明结论;
③在②的前提下,连接![]() ,点
,点![]() 是坐标平面内的点,若以
是坐标平面内的点,若以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 全等,请直接写出点
全等,请直接写出点![]() 的坐标.
的坐标.
【答案】(1)点![]() 的坐标为
的坐标为![]() ,
,![]() ;(2)①
;(2)①![]() ;②点F的坐标为
;②点F的坐标为![]() ,四边形
,四边形![]() 为正方形,证明见解析;③点
为正方形,证明见解析;③点![]() 的坐标为
的坐标为![]() 或
或![]() 或
或![]() .
.
【解析】
(1)根据已知条件与旋转的性质证明![]() ,根据全等三角形的性质得出点C的坐标,结合点E的坐标,根据待定系数法求出抛物线的表达式;
,根据全等三角形的性质得出点C的坐标,结合点E的坐标,根据待定系数法求出抛物线的表达式;
(2)①设直线AC的表达式为![]() ,由点A、C的坐标求出直线AC的表达式,进而得解;
,由点A、C的坐标求出直线AC的表达式,进而得解;
②过点![]() 作
作![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴,垂足为点
轴,垂足为点![]() ,
,![]() 的延长线与
的延长线与![]() 的延长线交于点
的延长线交于点![]() ,根据等腰三角形三线合一得出
,根据等腰三角形三线合一得出![]() ,结合①由平行线分线段成比例得出点G的坐标,根据待定系数法求出直线
,结合①由平行线分线段成比例得出点G的坐标,根据待定系数法求出直线![]() 的表达式,结合抛物线的表达式求出点F;利用勾股定理求出
的表达式,结合抛物线的表达式求出点F;利用勾股定理求出![]() ,结合
,结合![]() 可得出结论;
可得出结论;
③根据直线AC的表达式求出点H的坐标,设点N坐标为![]() ,根据勾股定理分别求出
,根据勾股定理分别求出![]() ,
,![]() ,
,![]() ,
,![]() ,然后分两种情况考虑:若△FHC≌△FHN,则FN=FC,NH=CH,若△FHC≌△HFN,则FN=CH,NH=FC,分别列式求解即可.
,然后分两种情况考虑:若△FHC≌△FHN,则FN=FC,NH=CH,若△FHC≌△HFN,则FN=CH,NH=FC,分别列式求解即可.
解:(1)![]() ,
,![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,
![]() 线段
线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到线段
得到线段![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
![]() 轴于点
轴于点![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() ,
,
∵抛物线![]() 的图象经过点
的图象经过点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,
![]() ,
,
解得, ,
,
∴抛物线的表达式为![]() ;
;
(2)①设直线AC的表达式为![]() ,
,
∵直线AC经过点![]() ,
,![]() ,
,
∴![]() ,
,
解得, ,即
,即![]() ,
,
∴点![]() 的纵坐标用含
的纵坐标用含![]() 的代数式表示为:
的代数式表示为:![]() ,
,
故答案为:![]() .
.
②过点![]() 作
作![]() 轴于点
轴于点![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() 点
点![]() 为
为![]() ,
,
设直线![]() 的表达式为
的表达式为![]() ,将
,将![]() 和
和![]() 代入表达式得,
代入表达式得,![]() ,
,
![]() ,即表达式为
,即表达式为![]() ,
,
![]() 点
点![]() 为直线
为直线![]() 和抛物线的交点,
和抛物线的交点,
![]() 得
得![]() ,
,
![]() ,
,![]() (舍去),
(舍去),
![]() 点
点![]() 的坐标为
的坐标为![]() ,
,
过点![]() 作
作![]() 轴,垂足为点
轴,垂足为点![]() ,
,![]() 的延长线与
的延长线与![]() 的延长线交于点
的延长线交于点![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
在![]() 中和
中和![]() 中,根据勾股定理,得
中,根据勾股定理,得![]() ,
,
同理可得![]() ,
,
![]() ,
,
![]() 四边形
四边形![]() 为菱形,
为菱形,
![]() ,
,
![]() 菱形
菱形![]() 为正方形;
为正方形;
③∵直线AC:![]() 与x轴交于点H,
与x轴交于点H,
∴![]() ,
,
解得,x=12,
∴![]() ,
,
∴![]() ,
,![]() ,
,
设点N坐标为![]() ,
,
∴![]() ,
,![]() ,
,
第一种情况:若△FHC≌△FHN,则FN=FC,NH=CH,
∴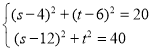 ,
,
解得,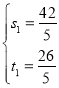 ,
,![]() (即点C),
(即点C),
∴![]() ;
;
第二种情况:若△FHC≌△HFN,则FN=CH,NH=FC,
∴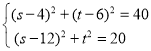 ,
,
解得,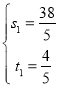 ,
,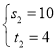 ,
,
∴![]() 或
或![]() ,
,
综上所述,以F,H,N为顶点的三角形与△FHC全等时,点N坐标为![]() 或
或![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
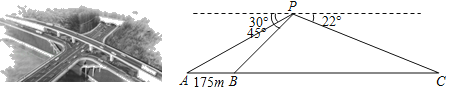
【题目】横卧于清波之上的黄石大桥与已经贯通的五峰山隧道将成为恩施城区跨越东西方向的最大直线通道,它把六角亭老城区与知名景点女儿城连为一体,缓解了恩施城区交通拥堵的现状.如图,某数学兴趣小组利用无人机在五峰山隧道正上空点P处测得黄石大桥西端点A的俯角为30°,东端点B(隧道西进口)的俯角为45°,隧道东出口C的俯角为22°,已知黄石大桥AB全长175米,隧道BC的长约多少米(计算结果精确到1米)?(参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,![]() 1.4,
1.4,![]() 1.7)
1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】伊利集团是中国规模最大、产品线最全的乳制品企业.综合实践小组的同学从网上搜集到如下一些伊利集团近几年的营业状况的资料,其中图1是2013﹣2018年伊利集团营业收入及净利润情况统计图,图2是2018年伊利集团各品类业务营收比例情况统计图(数据来源:公司财报、中商产业研究院).
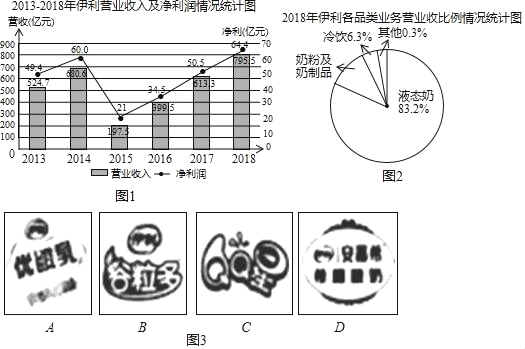
(1)解读信息:
综合实践小组的同学结合统计图提出了如下问题,请你解答:
①2018年,伊利集团营收及净利再次刷新行业纪录,稳居亚洲乳业第一.这一年,伊利集团实现营业收人 亿元,净利润 亿元;
②求2018年伊利集团“奶粉及奶制品“业务的营业收入(结果保留整数);
③在2013﹣2018这6年中;伊利集团净利润比上一年增长额最多的是 年;估计2019年伊利集团的净利润将比上一年增长 亿元,理由是 ;
(2)拓展活动:
如图,同学们收集了伊利集团旗下“优酸乳、谷粒多、QQ星,安幕希”四种产品的商标图片(四张图片除商标图案外完全相同,分别记为A,B,C,D)(见图3).同学们用这四张卡片设计了一个游戏,规则是:将四张图片背面朝上放在桌上,搅匀后,由甲从中随机抽取一张,记下商标名称后放回;再次搅匀后,由乙从中随机抽取一张.若两人抽到的商标相同则甲获胜;否则,乙获胜,这个规则对甲乙双方公平吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=a.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.
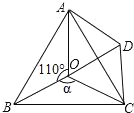
(1)试说明△COD是等边三角形;
(2)当a=150°时,OB=3,OC=4,试求OA的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在课外实践中,小明为了测量江中信号塔![]() 离河边的距离
离河边的距离![]() ,采取了如下措施:如图在江边
,采取了如下措施:如图在江边![]() 处,测得信号塔
处,测得信号塔![]() 的俯角为
的俯角为![]() ,若
,若![]() 米,
米,![]() ,
,![]() 米,
米,![]() 平行于
平行于![]() ,
,![]() 的坡度为
的坡度为![]() ,坡长
,坡长![]() 米,则
米,则![]() 的长为( )(精确到0.1米,参考数据:
的长为( )(精确到0.1米,参考数据:![]() ,
,![]() ,
,![]() )
)
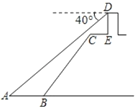
A.78.6米B.78.7米C.78.8米D.78.9米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y = ![]() ax2 ax + c图象的顶点为C,一次函数y = x + 3的图象与这个二次函数的图象交于A、B两点(其中点A在点B的左侧),与它的对称轴交于点D.
ax2 ax + c图象的顶点为C,一次函数y = x + 3的图象与这个二次函数的图象交于A、B两点(其中点A在点B的左侧),与它的对称轴交于点D.
(1)求点D的坐标;
(2) ①若点C与点D关于x轴对称,且△BCD的面积等于4,求此二次函数的关系式;
②若CD=DB,且△BCD的面积等于4![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
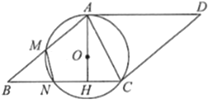
【题目】如图,点O是线段AH上一点,AH=3,以点O为圆心,OA的长为半径作⊙O,过点H作AH的垂线交⊙O于C,N两点,点B在线段CN的延长线上,连接AB交⊙O于点M,以AB,BC为边作ABCD.
(1)求证:AD是⊙O的切线;
(2)若OH![]() AH,求四边形AHCD与⊙O重叠部分的面积;
AH,求四边形AHCD与⊙O重叠部分的面积;
(3)若NH![]() AH,BN
AH,BN![]() ,连接MN,求OH和MN的长.
,连接MN,求OH和MN的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com