
【题目】在课外实践中,小明为了测量江中信号塔![]() 离河边的距离
离河边的距离![]() ,采取了如下措施:如图在江边
,采取了如下措施:如图在江边![]() 处,测得信号塔
处,测得信号塔![]() 的俯角为
的俯角为![]() ,若
,若![]() 米,
米,![]() ,
,![]() 米,
米,![]() 平行于
平行于![]() ,
,![]() 的坡度为
的坡度为![]() ,坡长
,坡长![]() 米,则
米,则![]() 的长为( )(精确到0.1米,参考数据:
的长为( )(精确到0.1米,参考数据:![]() ,
,![]() ,
,![]() )
)
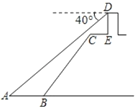
A.78.6米B.78.7米C.78.8米D.78.9米
 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 为
为![]() 边上一点,且
边上一点,且![]() .点
.点![]() 从点
从点![]() 出发.沿射线
出发.沿射线![]() 以每秒1个单位长度的速度运动.以
以每秒1个单位长度的速度运动.以![]() 、
、![]() 为邻边作
为邻边作![]() .设
.设![]() 和
和![]() 重叠部分图形的面积为
重叠部分图形的面积为![]() (平方单位),点
(平方单位),点![]() 的运动时间为
的运动时间为![]() (秒)
(秒)![]() .
.
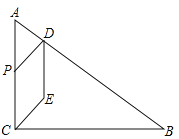
(1)连结![]() ,求
,求![]() 的长.
的长.
(2)当![]() 为菱形时,求
为菱形时,求![]() 的值.
的值.
(3)求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(4)将线段![]() 沿直线
沿直线![]() 翻折得到线段
翻折得到线段![]() .当点
.当点![]() 落在
落在![]() 的边上时,直接写出
的边上时,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
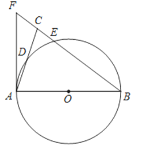
【题目】如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC,BC于点D,E,BC的延长线与⊙O的切线AF交于点F.
(1)求证:∠ABC=2∠CAF;
(2)若AC=2![]() ,CE:EB=1:4,求CE,AF的长.
,CE:EB=1:4,求CE,AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
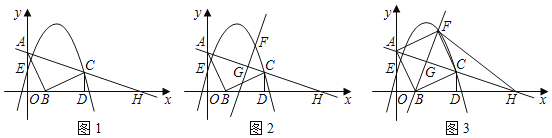
【题目】综合与探究:
如图1,![]() 的直角顶点
的直角顶点![]() 在坐标原点,点
在坐标原点,点![]() 在
在![]() 轴正半轴上,点
轴正半轴上,点![]() 在
在![]() 轴正半轴上,
轴正半轴上,![]() ,
,![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到线段
得到线段![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,抛物线
,抛物线![]() 经过点
经过点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
(1)求点![]() 的坐标及抛物线的表达式;
的坐标及抛物线的表达式;
(2)如图2,已知点![]() 是线段
是线段![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 的垂线交抛物线于点
的垂线交抛物线于点![]() (点
(点![]() 在第一象限),设点
在第一象限),设点![]() 的横坐标为
的横坐标为![]() .
.
①点![]() 的纵坐标用含
的纵坐标用含![]() 的代数式表示为________;
的代数式表示为________;
②如图3,当直线![]() 经过点
经过点![]() 时,求点
时,求点![]() 的坐标,判断四边形
的坐标,判断四边形![]() 的形状并证明结论;
的形状并证明结论;
③在②的前提下,连接![]() ,点
,点![]() 是坐标平面内的点,若以
是坐标平面内的点,若以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 全等,请直接写出点
全等,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图4所示,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从点A出发沿边AC向点C以1cm/s的速度移动,点Q从C点出发沿CB边向点B以2cm/s的速度移动.
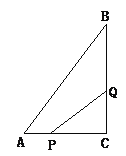
(1)、如果P、Q同时出发,几秒钟后,可使△PCQ的面积为8平方厘米?
(2)、点P、Q在移动过程中,是否存在某一时刻,使得△PCQ的面积等于△ABC的面积的一半.若存在,求出运动的时间;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了增强学生对新冠病毒预防知识的了解,我校初一年级开展了网上预防知识的宣传教育活动.为了解这次宣传教育活动的效果,学校从初一年级1500名学生中随机抽取部分学生进行网上知识测试(测试满分100分,得分均为整数),并根据抽取的学生测试成绩,制作了如下统计图表:
抽取学生知识测试成绩的频数表 | ||
成绩 | 频数(人) | 频率 |
| 10 | 0.1 |
| 15 |
|
|
| 0.2 |
| 40 |
|
|
|
|
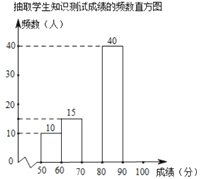
由图表中给出的信息回答下列问题:
(1)![]() ,
,![]() ,并补全频数直方图;
,并补全频数直方图;
(2)如果80分以上(包括80分)为优秀,请估计初一年级1500名学生中成绩优秀的人数;
(3)小强在这次测试中成绩为85分,你认为85分一定是这100名学生知识测试成绩的中位数吗?请简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2021年我省开始实施“ 3+1+2”高考新方案,其中语文、数学、外语三门为统考科目( 必考), 物理和历史两个科目中任选 1门,另外在思想政治、地理、化学、生物四门科目中任选 2门,共计6门科目,总分750 分, 假设小丽在选择科目时不考虑主观性.
(1)小丽选到物理的概率为 ;
(2)请用“画树状图”或“列表”的方法分析小丽在思想政治、 地理、 化学、生物四门科目中任选 2门选到化学、生物的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知, ![]() ,
, ![]() 与
与![]() 成正比例,
成正比例, ![]() 与
与![]() 成反比例,并且当
成反比例,并且当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() .
.
(![]() )求
)求![]() 关于
关于![]() 的函数关系式.
的函数关系式.
(![]() )当
)当![]() 时,求
时,求![]() 的值.
的值.
【答案】(![]() )
)![]() ;(
;(![]() )
)![]() ,
, ![]() .
.
【解析】分析:(1)首先根据![]() 与x成正比例,
与x成正比例, ![]() 与x成反比例,且当x=1时,y=4;当x=2时,y=5,求出
与x成反比例,且当x=1时,y=4;当x=2时,y=5,求出![]() 和
和![]() 与x的关系式,进而求出y与x的关系式,(2)根据(1)问求出的y与x之间的关系式,令y=0,即可求出x的值.
与x的关系式,进而求出y与x的关系式,(2)根据(1)问求出的y与x之间的关系式,令y=0,即可求出x的值.
本题解析:
(![]() )设
)设![]() ,
, ![]() ,
,
则![]() ,
,
∵当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,
,
∴
解得, ![]() ,
,
∴![]() 关于
关于![]() 的函数关系式为
的函数关系式为![]() .
.
(![]() )把
)把![]() 代入
代入![]() 得,
得,
![]() ,
,
解得: ![]() ,
, ![]() .
.
点睛:本题考查了用待定系数法求反比例函数的解析式:(1)设出含有待定系数的反比例函数解析式y=kx(k为常数,k≠0);(2)把已知条件(自变量与对应值)代入解析式,得到待定系数的方程;(3)解方程,求出待定系数;(4)写出解析式.
【题型】解答题
【结束】
24
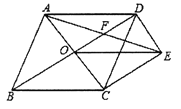
【题目】如图,菱形![]() 的对角线
的对角线![]() 、
、![]() 相交于点
相交于点![]() ,过点
,过点![]() 作
作![]() 且
且![]() ,连接
,连接![]() 、
、![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.
(1)求证:![]() ;
;
(2)若菱形![]() 的边长为2,
的边长为2, ![]() .求
.求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com