
【题目】2021年我省开始实施“ 3+1+2”高考新方案,其中语文、数学、外语三门为统考科目( 必考), 物理和历史两个科目中任选 1门,另外在思想政治、地理、化学、生物四门科目中任选 2门,共计6门科目,总分750 分, 假设小丽在选择科目时不考虑主观性.
(1)小丽选到物理的概率为 ;
(2)请用“画树状图”或“列表”的方法分析小丽在思想政治、 地理、 化学、生物四门科目中任选 2门选到化学、生物的概率.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() .
.

(1)如图①,点![]() 在斜边
在斜边![]() 上,以点
上,以点![]() 为圆心,
为圆心,![]() 长为半径的圆交
长为半径的圆交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,与边
,与边![]() 相切于点
相切于点![]() .求证:
.求证:![]() ;
;
(2)在图②中作![]() ,使它满足以下条件:
,使它满足以下条件:
①圆心在边![]() 上;②经过点
上;②经过点![]() ;③与边
;③与边![]() 相切.
相切.
(尺规作图,只保留作图痕迹,不要求写出作法)
查看答案和解析>>
科目:初中数学 来源: 题型:
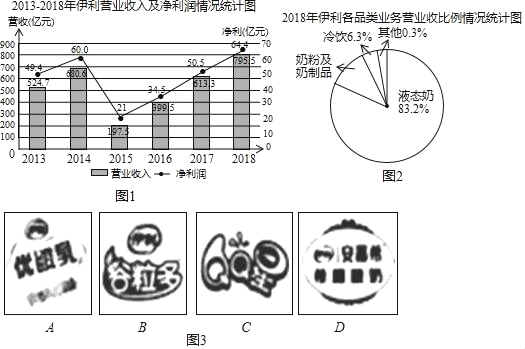
【题目】伊利集团是中国规模最大、产品线最全的乳制品企业.综合实践小组的同学从网上搜集到如下一些伊利集团近几年的营业状况的资料,其中图1是2013﹣2018年伊利集团营业收入及净利润情况统计图,图2是2018年伊利集团各品类业务营收比例情况统计图(数据来源:公司财报、中商产业研究院).
(1)解读信息:
综合实践小组的同学结合统计图提出了如下问题,请你解答:
①2018年,伊利集团营收及净利再次刷新行业纪录,稳居亚洲乳业第一.这一年,伊利集团实现营业收人 亿元,净利润 亿元;
②求2018年伊利集团“奶粉及奶制品“业务的营业收入(结果保留整数);
③在2013﹣2018这6年中;伊利集团净利润比上一年增长额最多的是 年;估计2019年伊利集团的净利润将比上一年增长 亿元,理由是 ;
(2)拓展活动:
如图,同学们收集了伊利集团旗下“优酸乳、谷粒多、QQ星,安幕希”四种产品的商标图片(四张图片除商标图案外完全相同,分别记为A,B,C,D)(见图3).同学们用这四张卡片设计了一个游戏,规则是:将四张图片背面朝上放在桌上,搅匀后,由甲从中随机抽取一张,记下商标名称后放回;再次搅匀后,由乙从中随机抽取一张.若两人抽到的商标相同则甲获胜;否则,乙获胜,这个规则对甲乙双方公平吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在课外实践中,小明为了测量江中信号塔![]() 离河边的距离
离河边的距离![]() ,采取了如下措施:如图在江边
,采取了如下措施:如图在江边![]() 处,测得信号塔
处,测得信号塔![]() 的俯角为
的俯角为![]() ,若
,若![]() 米,
米,![]() ,
,![]() 米,
米,![]() 平行于
平行于![]() ,
,![]() 的坡度为
的坡度为![]() ,坡长
,坡长![]() 米,则
米,则![]() 的长为( )(精确到0.1米,参考数据:
的长为( )(精确到0.1米,参考数据:![]() ,
,![]() ,
,![]() )
)
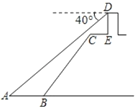
A.78.6米B.78.7米C.78.8米D.78.9米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小程经营的是一家服装店,店里有一款毛衣和一款牛仔裤销售非常可观,从2019年1月开店以来,平均每天可卖出毛衣10件,牛仔裤20件.已知道买1件毛衣和3件牛仔裤与买2件毛衣和1件牛仔裤需要的钱一样多,都为500元.
(1)买一件毛衣和一件牛仔裤各需要多少钱?
(2)双“十一”将至,小程经营的网店提前对该毛衣和牛仔裤开启了促销活动,活动当天,毛衣每件售价降低了![]() ,销售量在原来的基础上上涨
,销售量在原来的基础上上涨![]() ,仔裤每件售价也降低了
,仔裤每件售价也降低了![]() ,但销售量和原来一样,当天,这两件商品总的销售额为3960元,求
,但销售量和原来一样,当天,这两件商品总的销售额为3960元,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y = ![]() ax2 ax + c图象的顶点为C,一次函数y = x + 3的图象与这个二次函数的图象交于A、B两点(其中点A在点B的左侧),与它的对称轴交于点D.
ax2 ax + c图象的顶点为C,一次函数y = x + 3的图象与这个二次函数的图象交于A、B两点(其中点A在点B的左侧),与它的对称轴交于点D.
(1)求点D的坐标;
(2) ①若点C与点D关于x轴对称,且△BCD的面积等于4,求此二次函数的关系式;
②若CD=DB,且△BCD的面积等于4![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
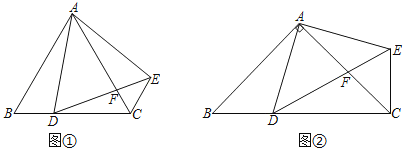
【题目】如图①,在△ABC中,AB=AC,∠BAC=60°,D为BC边上一点(不与点B,C重合),将线段AD绕点A逆时针旋转60°得到AE,连接EC,则:
(1)①∠ACE的度数是 ; ②线段AC,CD,CE之间的数量关系是 .
(2)如图②,在△ABC中,AB=AC,∠BAC=90°,D为BC边上一点(不与点B,C重合),将线段AD绕点A逆时针旋转90°得到AE,连接EC,请判断线段AC,CD,CE之间的数量关系,并说明理由;
(3)如图②,AC与DE交于点F,在(2)条件下,若AC=8,求AF的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
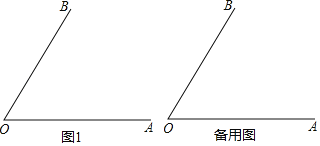
【题目】已知∠AOB=60°,P为它的内部一点,M为射线OA上一点,连接PM,以P为中心,将线段PM顺时针旋转120°,得到线段PN,并且点N恰好落在射线OB上.
(1)依题意补全图1;
(2)证明:点P一定落在∠AOB的平分线上;
(3)连接OP,如果OP=2![]() ,判断OM+ON的值是否变化,若发生变化,请求出值的变化范围,若不变,请求出值.
,判断OM+ON的值是否变化,若发生变化,请求出值的变化范围,若不变,请求出值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com